How to Calculate Annualized Portfolio Return

Time-Weighted Rate of Return

Find the difference between the beginning and ending values for each year. Subtract the value of the portfolio at the beginning of the year from the value of the portfolio at the end of the year, then divide that number by the value at the beginning of the year. This is your simple, or basic, rate of return. Multiply by 100 to find the percentage. For example, if the beginning value of your portfolio was $100,000 and your ending value was $105,000, your simple rate of return for that year would be 5%: ( 105 , 000 − 100 , 000 ) 100 , 000 = 0.05 x 100 = 5 % {\displaystyle {\frac {(105,000-100,000)}{100,000}}=0.05x100=5\%} {\displaystyle {\frac {(105,000-100,000)}{100,000}}=0.05x100=5\%} If you earned any dividends, include those in your ending value. In the previous example, if you'd also earned $50 in dividends, your ending value would be $105,050.

Add 1 to each rate and multiply them together. Start by adding 1 to each basic rate of return you've calculated for each year. Then, multiply those figures together to calculate the return for the entire time frame. This incorporates the way the value of your portfolio builds on itself, or compounds over time. For example, suppose you've had your portfolio for 4 years and your simple rates of return are 5% (0.05), 7% (0.07), 2% (0.02), and 4% (0.04). Your total return would be 1.19 (rounded): ( 1 + 0.05 ) x ( 1 + 0.07 ) x ( 1 + 0.02 ) x ( 1 + 0.04 ) = 1.1918 {\displaystyle (1+0.05)x(1+0.07)x(1+0.02)x(1+0.04)=1.1918} {\displaystyle (1+0.05)x(1+0.07)x(1+0.02)x(1+0.04)=1.1918}

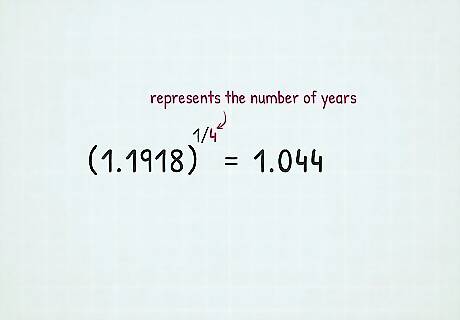
Raise the total rate by an exponent of 1/n. In the exponent position, "n" represents the number of years you included in your calculations. You're trying to find the average for any 1 of those years, so the exponent is represented as a fraction of 1 over the number of years. Continuing with the previous example, plug 1.1918 into your calculator and multiply by the exponent 1/4. Your answer should be 1.044. This calculation gets you a geometric average, which is simply an average of all the simple rates of return that also takes into account the compounding that occurs year after year.

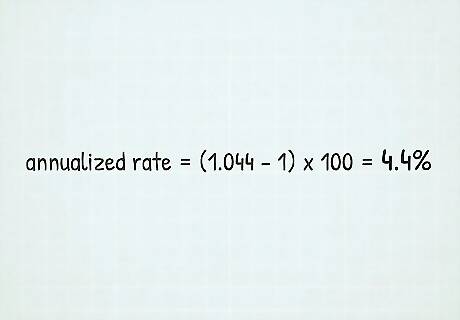
Subtract 1 and multiply by 100 to get the annualized rate of return. Now that you have your geometric average, you need to turn it into a percentage. Subtract 1 (this takes care of the 1s you previously added to each yearly return) to get your decimal. Then, multiply 100 to get your percentage. To continue with the example, your annualized rate would be 4.4%: ( 1.044 − 1 ) x 100 = 4.4 % {\displaystyle (1.044-1)x100=4.4\%} {\displaystyle (1.044-1)x100=4.4\%} The full formula is ( ( ( 1 + R 1 ) x ( 1 + R 2 ) x ( 1 + R 3 ) x ( 1 + R 4 ) ) 1 n − 1 ) x 100 {\displaystyle (((1+R_{1})x(1+R_{2})x(1+R_{3})x(1+R_{4}))^{\frac {1}{n}}-1)x100} {\displaystyle (((1+R_{1})x(1+R_{2})x(1+R_{3})x(1+R_{4}))^{\frac {1}{n}}-1)x100}, where "R" is the rate of return for each investment period and "n" is the number of years.

Use a different formula if you only have the initial and final values. To calculate the annualized portfolio return, divide the final value by the initial value, then raise that number by 1/n, where "n" is the number of years you held the investments. Then, subtract 1 and multiply by 100. For example, suppose your portfolio's initial value was $100,000 and the final value after 10 years is $150,000. Divide 150,000 by 100,000 to get 1.5. Then apply to 1.5 the exponent 1/10 to get 1.04. Subtract 1 to get 0.04, then multiply by 100. Your annualized rate of return is 4%: ( ( 150 , 000 / 100 , 000 ) 1 10 − 1 ) x 100 = 4 % {\displaystyle ((150,000/100,000)^{\frac {1}{10}}-1)x100=4\%} {\displaystyle ((150,000/100,000)^{\frac {1}{10}}-1)x100=4\%} The full formula is ( ( f i n a l v a l u e o f i n v e s t m e n t i n i t i a l v a l u e o f i n v e s t m e n t ) 1 n − 1 ) x 100 {\displaystyle (({\frac {\mathrm {final\ value\ of\ investment} }{\mathrm {initial\ value\ of\ investment} }})^{\frac {1}{n}}-1)x100} {\displaystyle (({\frac {\mathrm {final\ value\ of\ investment} }{\mathrm {initial\ value\ of\ investment} }})^{\frac {1}{n}}-1)x100}

Dollar-Weighted Rate of Return (IRR)

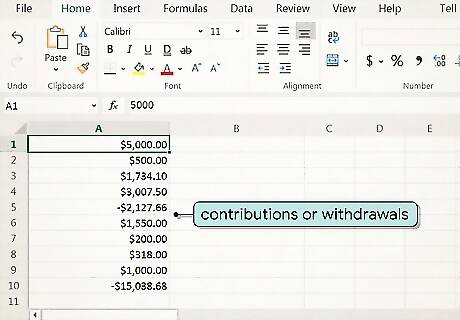
Enter your contributions or withdrawals in column A of a spreadsheet. Open a spreadsheet, then use column A to list each of your contributions or withdrawals to your portfolio, with your first value on row 1 (cell A1). Express withdrawals as negative numbers with a ( - ) in front of them. Put each contribution or withdrawal in a new cell. There's no need to combine cash flows for specific periods. For example, if you made 2 contributions and 1 withdrawal in a single year, you'd have 3 entries in 3 cells rather than just 1.

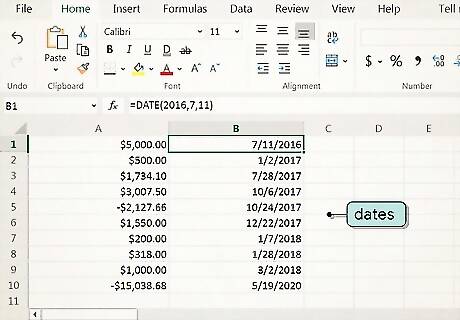
Put the dates of the contributions or withdrawals in column B. Next to the corresponding value in column A, type the date that contribution or withdrawal was made in column B. Use the "date" function so the program recognizes the values as dates. In Excel, the date function is =DATE(Year,Month,Day). For example, if you made a contribution on January 15, 2020, you would enter "=DATE(2020,1,15)".

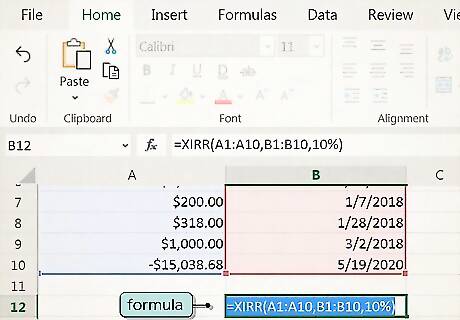
Input the formula on a new row. Once you've entered all of your data, drop down a row and add the formula =XIRR(values,dates,[guess]). The 3 variables in the formula break down like this: The values you enter refers to the range of cells containing the contributions or withdrawals you made. For example, if you used column A, rows 1 - 20, you would enter "A1:A20". For the dates, use the range of cells in the column containing your dates, using the same formula as you used for the values. For example, "B1:B20". The third value is your guess as to what you think the IRR will be. If you don't have a guess, you can leave this blank. Excel defaults to 10% if no guess is given.

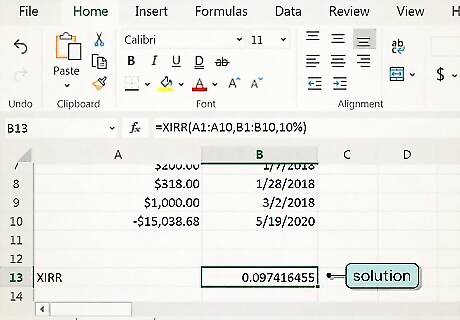
Allow the program to compute the solution in the same cell. Once you enter the formula in the cell, the program uses an iterative technique, which involves trying different rates in a complex equation until the correct one is found. These iterations start with your guess rate (or the default 10%) and move up or down to find the annualized dollar-weighted rate of return. The program will display the result in the same cell where you entered the formula. The result Excel and other spreadsheet programs reach is accurate within 0.000001%, so it's a result you can rely on.

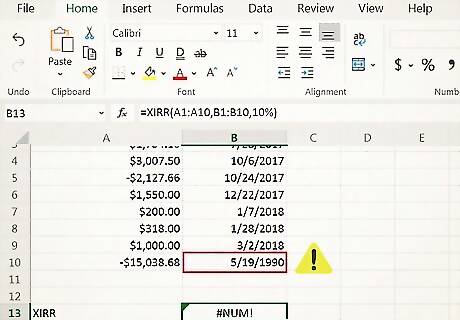
Troubleshoot your data if you get an error. If you enter the formula and get an error message instead of a result, it usually means there's something wrong with the data you entered. If you get a "#VALUE" error, it means you have a date that isn't recognized as a valid date. A "#NUM!" error could result from any of the following: Your value and date arrays are different lengths Your arrays don't contain at least 1 positive and at least 1 negative value One of your dates comes before the first date entered in your array The calculation failed to converge (find a result) after 100 iterations