How to Calculate Percentages

Calculating Percentage

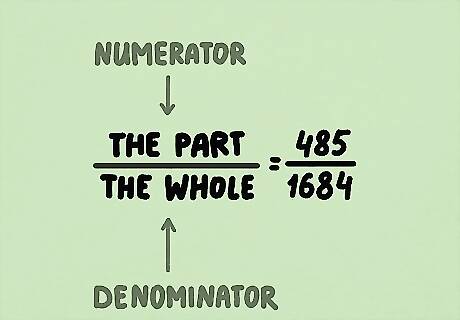
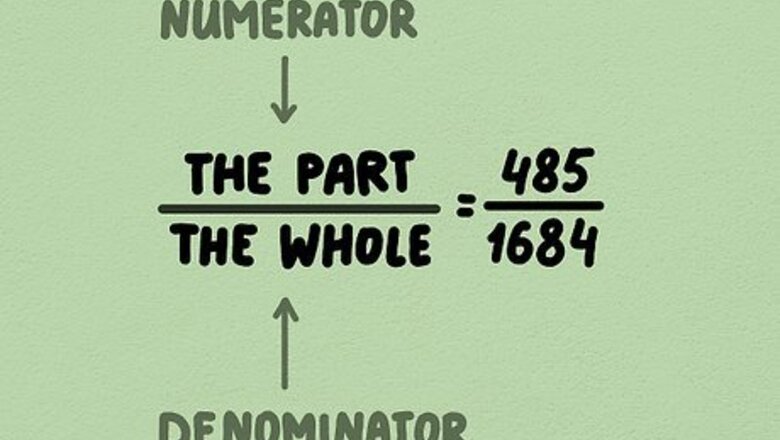
Put the two values into a fraction. The smaller part goes on top of the fraction (numerator), and the value of the whole goes on the bottom (denominator). For instance, let's say we have a jar containing 1199 red marbles and 485 blue marbles, making it 1684 marbles in total. If we’re looking to find the percentage of blue marbles, that is our “part.” The “whole” is the total number of marbles (1684). Therefore the fraction is 485/1684 (part/whole). When you're setting up two proportions, it's easiest to set them both up as the part over the whole on either side of the equation.

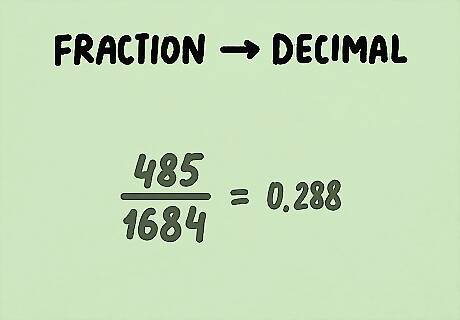
Convert the fraction into a decimal. Percentages are best calculated from the decimal form. For the marbles example, to turn 485/1684 into a decimal, divide 485 by 1684 using a calculator or pencil and paper. This comes to 0.288.

Convert the decimal into a percent. Multiply the result obtained in the step above by 100. For the marbles example, 0.288 multiplied by 100 equals 28.8%.• A simple way to multiply a decimal by 100 is to move the decimal to the right two digits.• The percent symbol is then just tacked on at the end, like a unit of measurement would be.

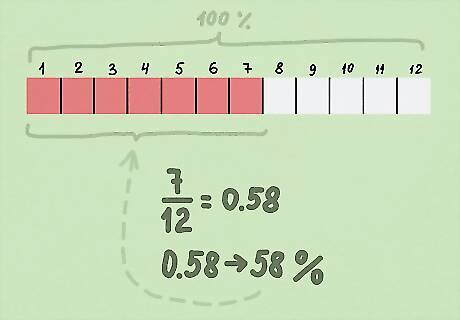
Bonus Example 1: Jerry, an electrician, worked 7 months out of the year. What percent of the year did he work? There are 12 months total in a year, so Jerry worked 7/12 months. Then, convert the fraction to a decimal: 7/12 = 0.58 Next, convert the fraction to a percent: 0.58 x 100% = 58% Jerry the electrician worked 58% of the year.

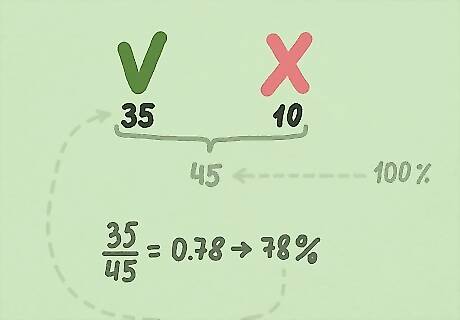
Bonus Example 2: Donovan took a math test and got 35 correct and 10 incorrect answers. What was the percentage of correct answers? 35 correct answers + 10 incorrect answers = 45 answers total We can set this problem up as the fraction 35/45. 35/45 = 0.78 0.78 x 100 = 78% Donovan got 78% of the answers correct on his test.

What Is X Percent of Y?

Use this method when you’re given a percentage and a “whole.” Set the numbers you’re given into the percent formula P/100 = Part/Whole. Say you borrowed money from a friend who is going to charge you daily interest. The amount borrowed was initially $15 and the interest rate is 3% per day. Then, 3% would be P in the formula, and $15 would be the “whole” amount. Plug the numbers into the formula to get 3/100 = X/15. Remember, part over whole equals part over whole.

Convert the percentage into a decimal. Divide the percentage by 100%, or you can multiply by 0.01 (they’re the exact same). 3%/100% = 3/100 = 0.03. You’d be left with 0.03=X/15.You can also simply move the decimal to the left two places. You can translate any percentage into a decimal by dividing by 100. For example, 26% = 26/100 = .26

Cross multiply to solve for X. It helps to reword your problem with the new value(s) now in the form of “X of Y is Z.” X is the decimal form of your percent, “of” means to multiply, Y is the whole amount, and Z is the answer. So, 0.03 x $15 is $0.45. In this example, $0.45 is the amount of interest accrued each day that you do not pay your friend back. If you need to further calculate the total due after 1 day, you would add the amount you borrowed to the amount of the interest times the number of days. So $15 + ($0.45 x 1 day) = $15.45.

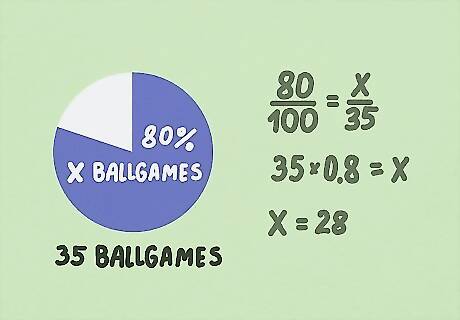
Bonus Example 1: A baseball pitcher won 80% of the games he pitched. If he pitched 35 ballgames, how many games did he win? We can reword this problem as “What is 80% of 35?” Plug the values into the formula P/100 = Part/Whole 80/100 = X/35 0.8 = X/35 35 x 0.8 = X X = 28 The pitcher won 28 games.

Bonus Example 2: A metal bar weighs 8.15 ounces. 93% of the bar is silver. How many ounces of silver are in the bar? We can reword this problem as “What is 93% of 8.15?” Plug the values into the formula P/100 = Part/Whole 93/100 = X/8.15 0.93 = X/8.15 0.93 x 8.15 = X X = 7.58 There are 7.58 ounces of silver.

P Percent of What Number Is Y?

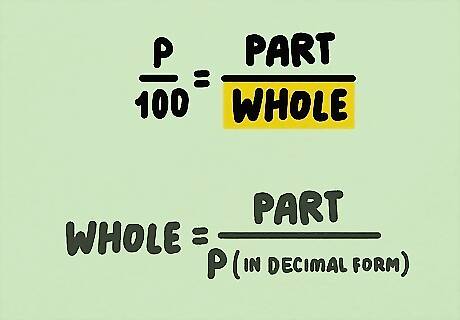
Use this method to solve for a missing “whole” when you’re given a percentage and a “part.” Set the numbers you’re given into the percent formula P/100 = Part/Whole, which we can write as P/100 = X/Y. For example, imagine you’re given the problem “45% of what number is 12?” Plug the numbers into the equation like this: 45/100 = 12/Y. A shortcut: notice you can manipulate the percent equation to get this formula below. Part/Percent (in decimal form) = Whole Keep reading for a full walk-through if you’re not sure how to get there.

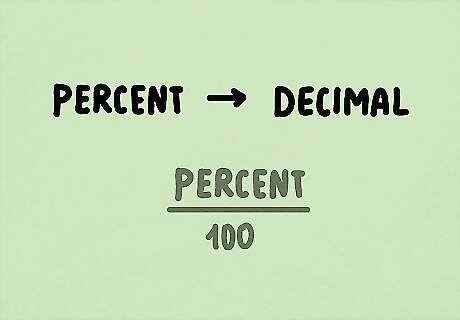
Convert the percentage into a decimal. Divide the percentage by 100, or just move the decimal place over 2 places to the left. 45%/100% = 45/100 = 0.45. You’ll end up with 0.45 = 12/Y.

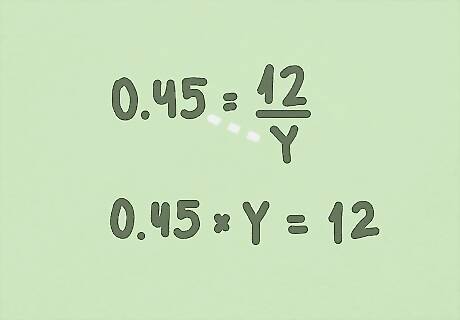
Cross multiply to move Y into the numerator. That means you’ll move from 0.45 = 12/Y to 0.45 x Y = 12. Now you can solve for your missing variable Y. In your head, you can reword this to “45 percent of Y is 12.” Remember “of” means "multiply."

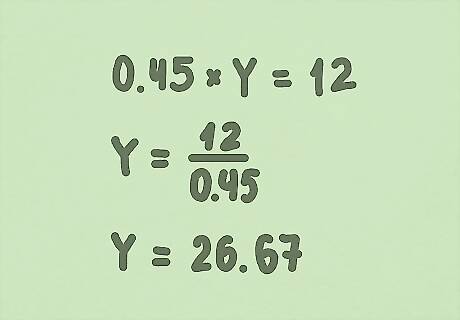
Divide the part by the percentage (in decimal form) to get your answer. For the main example, solve for Y by dividing both sides by 0.45. You’ll get Y = 12/0.45, which equals 26.67. For these types of problems, check your work by making sure that the answer is bigger than the original part you were given.

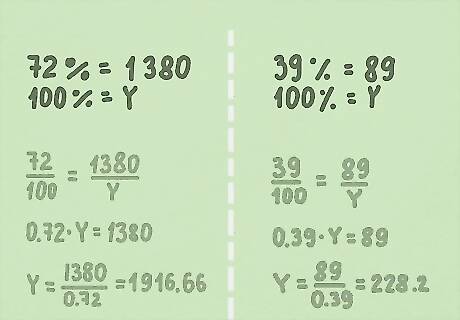
Check out these additional examples below. Bonus Example 1: This year, Acme Computers made approximately 72% of its sales online. There were 1,380 online purchases. Rounding up to the nearest whole number, how many total sales did Acme Computers make this year? Plug the values into the formula P/100 = Part/Whole 72/100 = 1,380 online sales/Y total sales 72/100 = 1,380/Y 0.72 = 1,380/Y 0.72 x Y = 1,380 1,380/0.72 = Y Y = 1916.66 Acme Computers made 1917 total sales this year. Bonus Example 2: 39% of what number is 89? Plug the values into the formula P/100 = Part/Whole 39/100 = 89/Y 0.39 = 89/Y 0.39 x Y = 89 89/0.39 = Y Y = 228.2

Calculating Percent Increase

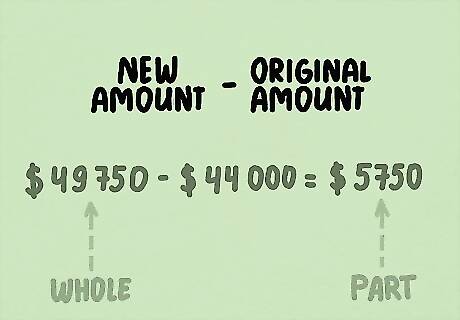
Subtract the original amount from the new, bigger amount. Imagine your small company makes $44,000 in one year. The next year, you make $49,750. To start calculating the percent change in revenue, find the difference between $49,750 and $44,000: $49,750 - $44,000 = $5,750. You’ll treat $5,750 as the “part” of the “whole” (which is your original number).

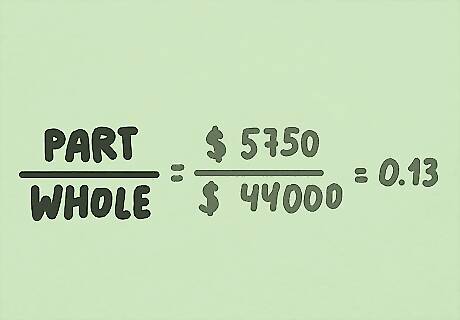
Divide the difference of the numbers by the original amount. You might recognize this as the first step in a basic percentage calculation–you’re setting up a fraction with the “part” over the “whole.” For the small business example, divide $5,750 by $44,000: $5,750 / $44,000 = 0.13.

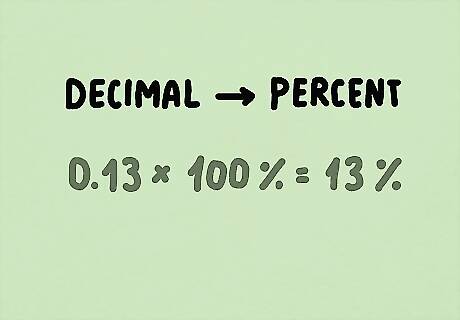
Multiply the decimal by 100% to get the percentage. You could also move the decimal place over twice to the right–it’s the same thing! In this case, we’d have 0.13 x 100% = 13%.

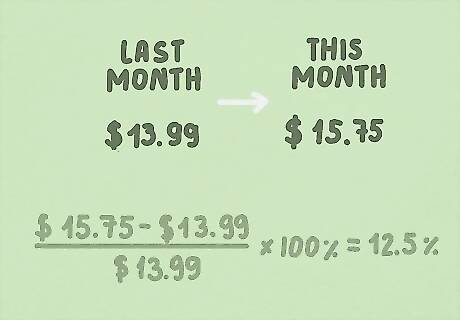
Bonus Example 1: A game cost $13.99 last month, but this month it costs $15.75. Calculate the percent increase of the price. New Amount - Original Amount = Difference $15.75 - $13.99 = $1.76 (Difference / Original Amount) x 100% = Percent Increase ($1.76 / $13.99) x 100% = 12.5% The price of the game went up by 12.5%.

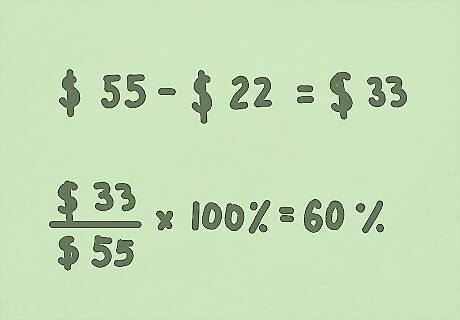
Bonus Example 2: A sweater company buys sweaters from a factory for $22. Then, they put their brand on the sweaters and sell them for $55. What’s the percentage of their markup (the difference in cost)? New Amount - Original Amount = Difference $55 - $22 = $33 (Difference / Original Amount) x 100% = Percent Increase ($33 / $55) x 100% = 60% The company has a 60% markup on sweaters.

Calculating Percent Decrease

Subtract the new amount from the original, bigger amount. For example, imagine you’re looking to invest in the stock market. A certain stock sold at $67 per share in one month. Now, the price has dropped to $52 per share. Subtract $52 from $67: $67 - $52 = $15. That $15 difference is the "part" of the "whole" ($67).

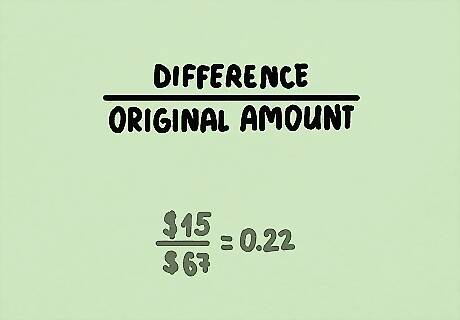
Divide the difference by the original amount. This is the basic percentage calculation–you’re essentially putting the “part” over the “whole” in fraction form. For the stock example, divide $67 by $15: $15 / $67 = 0.22.

Multiply the decimal by 100% to get the percentage. For a quick way to do this, move the decimal place over twice to the right. In this case, we’d have 0.22 x 100% = 22%.

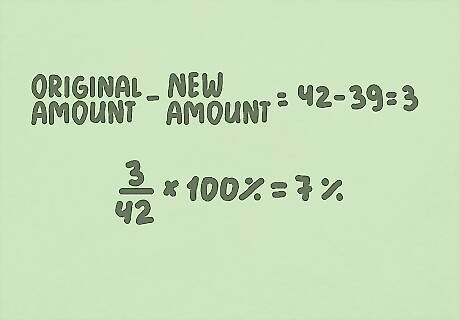
Bonus Example 1: Jane worked 42 hours a week in April. In May, she worked 39 hours a week. What was the percent change in her hours between the two months? Original Amount - New Amount = Difference 42 - 39 = 3 (Difference / Original Amount) x 100% = Percent Increase (3 / 42) x 100% = 7% Jane’s hours decreased by 7%.

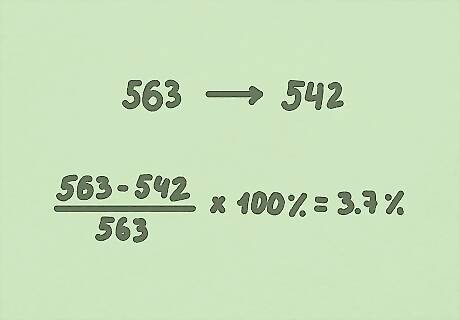
Bonus Example 2: Company A starts out with 563 employees. After layoffs, they’re left with 542 employees. What’s the percent change in the number of employees? Original Amount - New Amount = Difference 563 - 542 = 21 (Difference / Original Amount) x 100% = Percent Increase (21 / 563) x 100% = 3.7% Company A decreased their number of employees by 3.7%.

Percentage in Real Life

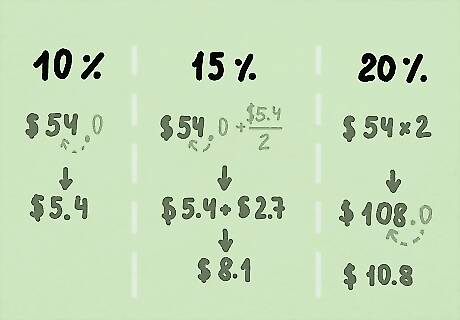
Calculate a restaurant tip in your head. You can calculate restaurant tips with tricks that involve moving the decimal place over for the total cost of your bill. Here are quick strategies to work out tip percentages without a calculator: Calculating a 10% tip: Simply move the decimal place over once to the left. Example: If your bill is $54, a 10% tip would be $5.4. Calculating a 15% tip: Find 10% by moving the decimal place over to the left. Then, divide that number in half to get 5% of the bill. Then, add the 10% and 5% values together. Example: For a $54 bill, 10% is $5.4. Half of $5.4 is $2.7. Finally, $5.4 + $2.7 = $8.1. Calculating a 20% tip: Double the total bill, then move the decimal place over once to the left. Example: For a $54 bill, double that is $108. If you move the decimal one place to the left, you'll get $10.80.

Calculate your savings from a price discount. Write down the original price and the discount percentage. Then, subtract the discount percentage from 100. For instance, if you want to buy a shirt that’s 30% off, 100% - 30% is 70%. That means you’ll pay 70% of the original price. Now you’re ready to walk through this easy calculation: Move the decimal two places to the left. In this example, 70%/100% = 70/100 = 7/10 = 0.7. Multiply the original price by the new decimal. If the shirt you want is $20, multiply $20 by 0.7. This comes to $14, meaning the shirt is now on sale for $14. Calculate your savings. Simply subtract the sale price from the original price ($20 - $14 = $6 saved)!

Calculate the total cost with sales tax. To calculate the cost of an item plus tax, start by converting the sales tax to a decimal. Next, add that number to 1 (think of 1 as 100% of the cost of the original item). For example, if sales tax is 8%, you’d do 0.08 + 1 = 1.08. Then, multiply the price of your item by 1.08. If your item costs $20, the item plus 8% tax would be $20 x 1.08, which equals $21.6. Bonus Example: Mark is buying a sweater that costs $15. Sales tax is 9%. How much will he pay at checkout? Convert 9% to a decimal: 0.09 Add the decimal to 1: 0.09 + 1 = 1.09 Multiple that value by the original price: $15 x 1.09 = $16.35 Mark will pay $16.35 at checkout.