
views
Preliminaries
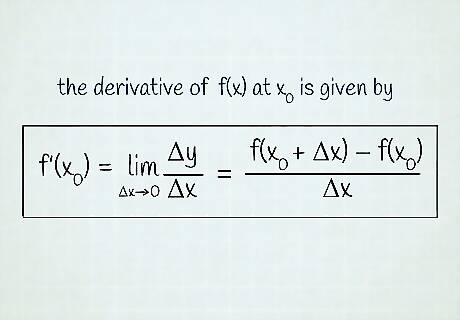
Understand the definition of the derivative. While this will almost never be used to actually take derivatives, an understanding of this concept is vital nonetheless. Recall that the linear function is of the form y = m x + b . {\displaystyle y=mx+b.} y=mx+b. To find the slope m {\displaystyle m} m of this function, two points on the line are taken, and their coordinates are plugged into the relation m = y 2 − y 1 x 2 − x 1 . {\displaystyle m={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}.} m={\frac {y_{{2}}-y_{{1}}}{x_{{2}}-x_{{1}}}}. Of course, this can only be used with linear graphs. For nonlinear functions, the line will be curved, so taking the difference of two points can only give the average rate of change between them. The line that intersects these two points is called the secant line, with a slope m = f ( x + Δ x ) − f ( x ) Δ x , {\displaystyle m={\frac {f(x+\Delta x)-f(x)}{\Delta x}},} m={\frac {f(x+\Delta x)-f(x)}{\Delta x}}, where Δ x = x 2 − x 1 {\displaystyle \Delta x=x_{2}-x_{1}} \Delta x=x_{{2}}-x_{{1}} is the change in x , {\displaystyle x,} x, and we have replaced y {\displaystyle y} y with f ( x ) . {\displaystyle f(x).} f(x). This is the same equation as the one before. The concept of the derivatives comes in when we take the limit Δ x → 0. {\displaystyle \Delta x\to 0.} \Delta x\to 0. When this happens, the distance between the two points shrinks, and the secant line better approximates the rate of change of the function. When we do send the limit to 0, we end up with the instantaneous rate of change and obtain the slope of the tangent line to the curve (see animation above). Then, we end up with the definition of the derivative, where the prime symbol denotes the derivative of the function f . {\displaystyle f.} f. f ′ ( x ) = lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x {\displaystyle f^{\prime }(x)=\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}} f^{{\prime }}(x)=\lim _{{\Delta x\to 0}}{\frac {f(x+\Delta x)-f(x)}{\Delta x}} Finding the derivative from this definition stems from expanding the numerator, canceling, and then evaluating the limit, since immediately evaluating the limit will give a 0 in the denominator.

Understand the derivative notation. There are two common notations for the derivative, though there are others. Lagrange's Notation. In the previous step, we used this notation to denote the derivative of a function f ( x ) {\displaystyle f(x)} f(x) by adding a prime symbol. f ′ ( x ) {\displaystyle f^{\prime }(x)} f^{{\prime }}(x) This notation is pronounced " f {\displaystyle f} f prime of x . {\displaystyle x.} x." To form higher order derivatives, simply add another prime symbol. When derivatives of fourth or higher order are taken, the notation becomes f ( 4 ) ( x ) , {\displaystyle f^{(4)}(x),} f^{{(4)}}(x), where this represents the fourth derivative. Leibniz's Notation. This is the other commonly used notation, and we will use it in the rest of the article. d f d x {\displaystyle {\frac {\mathrm {d} f}{\mathrm {d} x}}} {\frac {{\mathrm {d}}f}{{\mathrm {d}}x}} (For shorter expressions, the function can be placed in the numerator.) This notation literally means "the derivative of f {\displaystyle f} f with respect to x . {\displaystyle x.} x." It may be helpful to think of it as Δ y Δ x {\displaystyle {\frac {\Delta y}{\Delta x}}} {\frac {\Delta y}{\Delta x}} for values of x {\displaystyle x} x and y {\displaystyle y} y that are infinitesimally different from each other. When using this notation for higher derivatives, you must write d 2 f d x 2 , {\displaystyle {\frac {\mathrm {d} ^{2}f}{\mathrm {d} x^{2}}},} {\frac {{\mathrm {d}}^{{2}}f}{{\mathrm {d}}x^{{2}}}}, where this represents the second derivative. (Note that there "should" be parentheses in the denominator, but no one ever writes them, since everyone understands what we mean without them anyway.)
Basic Techniques
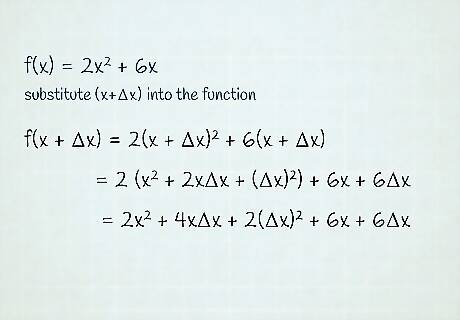
Substitute ( x + Δ x ) {\displaystyle (x+\Delta x)} (x+\Delta x) into the function. For this example, we will define f ( x ) = 2 x 2 + 6 x . {\displaystyle f(x)=2x^{2}+6x.} f(x)=2x^{{2}}+6x. f ( x + Δ x ) = 2 ( x + Δ x ) 2 + 6 ( x + Δ x ) = 2 ( x 2 + 2 x Δ x + ( Δ x ) 2 ) + 6 x + 6 Δ x = 2 x 2 + 4 x Δ x + 2 ( Δ x ) 2 + 6 x + 6 Δ x . {\displaystyle {\begin{aligned}f(x+\Delta x)&=2(x+\Delta x)^{2}+6(x+\Delta x)\\&=2(x^{2}+2x\Delta x+(\Delta x)^{2})+6x+6\Delta x\\&=2x^{2}+4x\Delta x+2(\Delta x)^{2}+6x+6\Delta x.\end{aligned}}} {\begin{aligned}f(x+\Delta x)&=2(x+\Delta x)^{{2}}+6(x+\Delta x)\\&=2(x^{{2}}+2x\Delta x+(\Delta x)^{{2}})+6x+6\Delta x\\&=2x^{{2}}+4x\Delta x+2(\Delta x)^{{2}}+6x+6\Delta x.\end{aligned}}
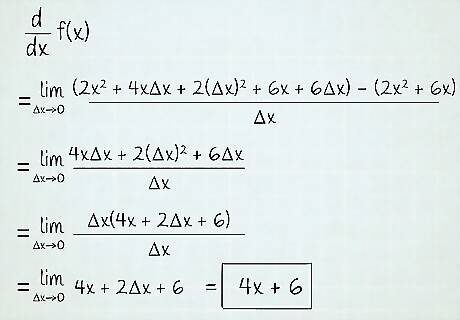
Substitute the function into the limit. Then evaluate the limit. d d x f ( x ) = lim Δ x → 0 ( 2 x 2 + 4 x Δ x + 2 ( Δ x ) 2 + 6 x + 6 Δ x ) − ( 2 x 2 + 6 x ) Δ x = lim Δ x → 0 4 x Δ x + 2 ( Δ x ) 2 + 6 Δ x Δ x = lim Δ x → 0 Δ x ( 4 x + 2 Δ x + 6 ) Δ x = lim Δ x → 0 4 x + 2 Δ x + 6 = 4 x + 6. {\displaystyle {\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} x}}f(x)&=\lim _{\Delta x\to 0}{\frac {(2x^{2}+4x\Delta x+2(\Delta x)^{2}+6x+6\Delta x)-(2x^{2}+6x)}{\Delta x}}\\&=\lim _{\Delta x\to 0}{\frac {4x\Delta x+2(\Delta x)^{2}+6\Delta x}{\Delta x}}\\&=\lim _{\Delta x\to 0}{\frac {\Delta x(4x+2\Delta x+6)}{\Delta x}}\\&=\lim _{\Delta x\to 0}4x+2\Delta x+6\\&=4x+6.\end{aligned}}} {\begin{aligned}{\frac {{\mathrm {d}}}{{\mathrm {d}}x}}f(x)&=\lim _{{\Delta x\to 0}}{\frac {(2x^{{2}}+4x\Delta x+2(\Delta x)^{{2}}+6x+6\Delta x)-(2x^{{2}}+6x)}{\Delta x}}\\&=\lim _{{\Delta x\to 0}}{\frac {4x\Delta x+2(\Delta x)^{2}+6\Delta x}{\Delta x}}\\&=\lim _{{\Delta x\to 0}}{\frac {\Delta x(4x+2\Delta x+6)}{\Delta x}}\\&=\lim _{{\Delta x\to 0}}4x+2\Delta x+6\\&=4x+6.\end{aligned}} This is a lot of work for such a simple function. We will see that there are plenty of derivative rules to skirt past this type of evaluation. You can find the slope anywhere on the function f ( x ) = 2 x 2 + 6 x . {\displaystyle f(x)=2x^{2}+6x.} f(x)=2x^{2}+6x. Simply plug in any x value into the derivative d f ( x ) d x = 4 x + 6. {\displaystyle {\frac {\mathrm {d} f(x)}{\mathrm {d} x}}=4x+6.} {\frac {{\mathrm {d}}f(x)}{{\mathrm {d}}x}}=4x+6.
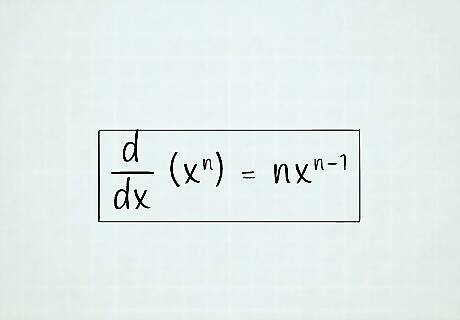
Use the power rule when f ( x ) {\displaystyle f(x)} f(x) is a polynomial function of degree n. Multiply the exponent with the coefficient and bring down the power by one. The formula is d d x ( x n ) = n x n − 1 . {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}(x^{n})=nx^{n-1}.} {\frac {{\mathrm {d}}}{{\mathrm {d}}x}}(x^{{n}})=nx^{{n-1}}. Although the intuitive method seems to only apply to natural number exponents, it can be generalized to all real numbers; that is, n ∈ R . {\displaystyle n\in \mathbb {R} .} n\in {\mathbb R}.
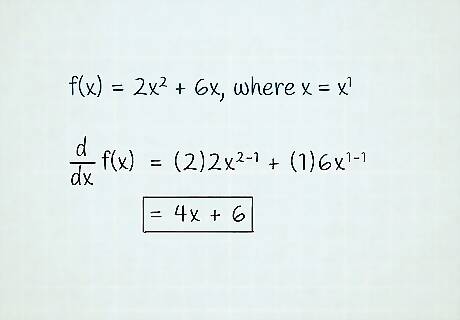
Use the previous example. f ( x ) = 2 x 2 + 6 x . {\displaystyle f(x)=2x^{2}+6x.} f(x)=2x^{{2}}+6x. Remember that x = x 1 . {\displaystyle x=x^{1}.} x=x^{{1}}. f ( x ) = 2 x 2 + 6 x d d x f ( x ) = ( 2 ) 2 x 2 − 1 + ( 1 ) 6 x 1 − 1 = 4 x + 6. {\displaystyle {\begin{aligned}f(x)&=2x^{2}+6x\\{\frac {\mathrm {d} }{\mathrm {d} x}}f(x)&=(2)2x^{2-1}+(1)6x^{1-1}\\&=4x+6.\end{aligned}}} {\begin{aligned}f(x)&=2x^{2}+6x\\{\frac {{\mathrm {d}}}{{\mathrm {d}}x}}f(x)&=(2)2x^{{2-1}}+(1)6x^{{1-1}}\\&=4x+6.\end{aligned}} We have used the property that the derivative of a sum is the sum of the derivatives (technically, the reason why we can do this is because the derivative is a linear operator). Obviously, the power rule makes finding derivatives of polynomials much easier. Before going on, it is important to note that the derivative of a constant is 0, because the derivative measures the rate of change, and no such change exists with a constant.

Differentiate again. Taking a higher order derivative of a function just means you take the derivative of the derivative (for order of 2). For example, if it asks you to take the third derivative, just differentiate the function three times. For polynomial functions of degree n , {\displaystyle n,} n, the n + 1 {\displaystyle n+1} n+1 order derivative will be 0.
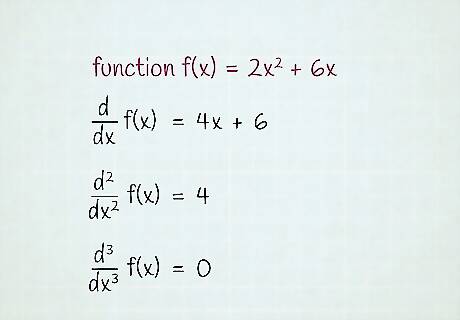
Take the third derivative of the previous example f ( x ) = 2 x 2 + 6 x {\displaystyle f(x)=2x^{2}+6x} f(x)=2x^{{2}}+6x. d d x f ( x ) = 4 x + 6 d 2 d x 2 f ( x ) = 4 d 3 d x 3 f ( x ) = 0 {\displaystyle {\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} x}}f(x)&=4x+6\\{\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}f(x)&=4\\{\frac {\mathrm {d} ^{3}}{\mathrm {d} x^{3}}}f(x)&=0\end{aligned}}} {\begin{aligned}{\frac {{\mathrm {d}}}{{\mathrm {d}}x}}f(x)&=4x+6\\{\frac {{\mathrm {d}}^{{2}}}{{\mathrm {d}}x^{{2}}}}f(x)&=4\\{\frac {{\mathrm {d}}^{{3}}}{{\mathrm {d}}x^{{3}}}}f(x)&=0\end{aligned}} In most applications of derivatives, especially in physics and engineering, you will at most differentiate twice, or perhaps three times.
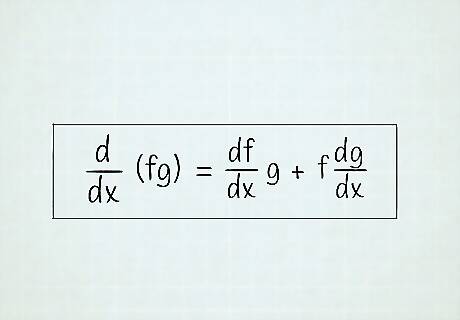
See this article for a full treatment on the product rule. In general, the derivative of a product does not equal the product of the derivatives. Rather, each function "gets its turn" to differentiate. d d x ( f g ) = d f d x g + f d g d x {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}(fg)={\frac {\mathrm {d} f}{\mathrm {d} x}}g+f{\frac {\mathrm {d} g}{\mathrm {d} x}}} {\frac {{\mathrm {d}}}{{\mathrm {d}}x}}(fg)={\frac {{\mathrm {d}}f}{{\mathrm {d}}x}}g+f{\frac {{\mathrm {d}}g}{{\mathrm {d}}x}}
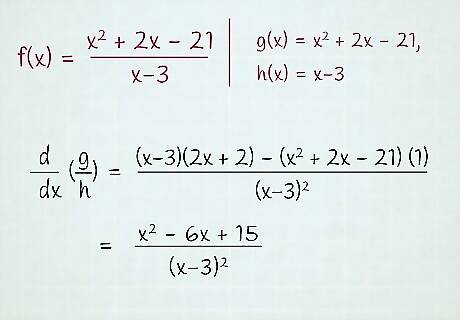
Use the quotient rule to take derivatives of rational functions. As with products in general, the derivative of a quotient does not equal the quotient of the derivatives. d d x ( f g ) = g d f d x − f d g d x g 2 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\left({\frac {f}{g}}\right)={\frac {g{\frac {\mathrm {d} f}{\mathrm {d} x}}-f{\frac {\mathrm {d} g}{\mathrm {d} x}}}{g^{2}}}} {\frac {{\mathrm {d}}}{{\mathrm {d}}x}}\left({\frac {f}{g}}\right)={\frac {g{\frac {{\mathrm {d}}f}{{\mathrm {d}}x}}-f{\frac {{\mathrm {d}}g}{{\mathrm {d}}x}}}{g^{{2}}}} A useful mnemonic for the numerator of the derivative is "Down-dee-up, up-dee-down," since the minus sign means the order matters. For example, consider the function f ( x ) = x 2 + 2 x − 21 x − 3 . {\displaystyle f(x)={\frac {x^{2}+2x-21}{x-3}}.} f(x)={\frac {x^{2}+2x-21}{x-3}}. Let g ( x ) = x 2 + 2 x − 21 {\displaystyle g(x)=x^{2}+2x-21} g(x)=x^{2}+2x-21 and h ( x ) = x − 3. {\displaystyle h(x)=x-3.} h(x)=x-3. Then use the quotient rule. d d x ( g h ) = ( x − 3 ) ( 2 x + 2 ) − ( x 2 + 2 x − 21 ) ( 1 ) ( x − 3 ) 2 = x 2 − 6 x + 15 ( x − 3 ) 2 {\displaystyle {\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} x}}\left({\frac {g}{h}}\right)&={\frac {(x-3)(2x+2)-(x^{2}+2x-21)(1)}{(x-3)^{2}}}\\&={\frac {x^{2}-6x+15}{(x-3)^{2}}}\end{aligned}}} {\begin{aligned}{\frac {{\mathrm {d}}}{{\mathrm {d}}x}}\left({\frac {g}{h}}\right)&={\frac {(x-3)(2x+2)-(x^{{2}}+2x-21)(1)}{(x-3)^{{2}}}}\\&={\frac {x^{{2}}-6x+15}{(x-3)^{{2}}}}\end{aligned}} Make sure your algebra is up to par. Derivatives involving quotients like these can quickly become cumbersome in terms of the algebra involved. This means you should be comfortable with factoring out constants and keeping track of negative signs.
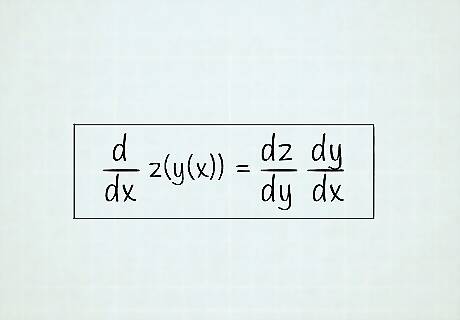
Use the chain rule for nested functions. For example, consider the scenario where z ( y ) {\displaystyle z(y)} z(y) is a differentiable function of y {\displaystyle y} y and y ( x ) {\displaystyle y(x)} y(x) is a differentiable function of x . {\displaystyle x.} x. Then there is a composite function z ( y ( x ) ) , {\displaystyle z(y(x)),} z(y(x)), or z {\displaystyle z} z as a function of x , {\displaystyle x,} x, that we can take the derivative of. d d x z ( y ( x ) ) = d z d y d y d x {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}z(y(x))={\frac {\mathrm {d} z}{\mathrm {d} y}}{\frac {\mathrm {d} y}{\mathrm {d} x}}} {\frac {{\mathrm {d}}}{{\mathrm {d}}x}}z(y(x))={\frac {{\mathrm {d}}z}{{\mathrm {d}}y}}{\frac {{\mathrm {d}}y}{{\mathrm {d}}x}} As with the product rule, this works with any number of functions; hence the "chain" rule. Here, an easy way to see how this works is if one imagines a d y d y {\displaystyle {\frac {\mathrm {d} y}{\mathrm {d} y}}} {\frac {{\mathrm {d}}y}{{\mathrm {d}}y}} inserted between d z d x . {\displaystyle {\frac {\mathrm {d} z}{\mathrm {d} x}}.} {\frac {{\mathrm {d}}z}{{\mathrm {d}}x}}.
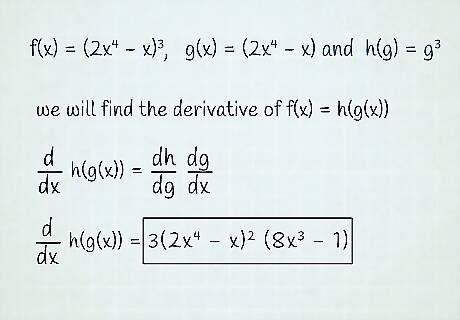
Consider the function f ( x ) = ( 2 x 4 − x ) 3 {\displaystyle f(x)=(2x^{4}-x)^{3}} f(x)=(2x^{{4}}-x)^{3}. Notice that this function can be decomposed into two elementary functions, g ( x ) = 2 x 4 − x {\displaystyle g(x)=2x^{4}-x} g(x)=2x^{{4}}-x and h ( g ) = g 3 . {\displaystyle h(g)=g^{3}.} h(g)=g^{{3}}. Then, we want to find the derivative of the composition f ( x ) = h ( g ( x ) ) . {\displaystyle f(x)=h(g(x)).} f(x)=h(g(x)). Use the chain rule d d x h ( g ( x ) ) = d h d g d g d x . {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}h(g(x))={\frac {\mathrm {d} h}{\mathrm {d} g}}{\frac {\mathrm {d} g}{\mathrm {d} x}}.} {\frac {{\mathrm {d}}}{{\mathrm {d}}x}}h(g(x))={\frac {{\mathrm {d}}h}{{\mathrm {d}}g}}{\frac {{\mathrm {d}}g}{{\mathrm {d}}x}}. We have now written the derivative in terms of derivatives that are easier to take. Then, d d x h ( g ( x ) ) = 3 ( 2 x 4 − x ) 2 ( 8 x 3 − 1 ) . {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}h(g(x))=3(2x^{4}-x)^{2}(8x^{3}-1).} {\frac {{\mathrm {d}}}{{\mathrm {d}}x}}h(g(x))=3(2x^{4}-x)^{2}(8x^{3}-1). With practice, you will see that applying the chain rule is easiest if you "peel away the onion." The first layer is everything inside the parentheses, cubed. The second layer is the function inside the parentheses. When dealing with more complex functions, this way of thinking helps to keep yourself on track and not get lost in what functions are taken with respect to what variables, etc.

See this article for a full treatment on implicit differentiation. Understanding the chain rule is a must in order to implicitly differentiate.

See this article for a full treatment on differentiating exponential functions. d d x e x = e x {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}e^{x}=e^{x}} {\frac {{\mathrm {d}}}{{\mathrm {d}}x}}e^{{x}}=e^{{x}} d d x a x = a x ln a {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}a^{x}=a^{x}\ln a} {\frac {{\mathrm {d}}}{{\mathrm {d}}x}}a^{{x}}=a^{{x}}\ln a d d x ln x = 1 x {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\ln x={\frac {1}{x}}} {\frac {{\mathrm {d}}}{{\mathrm {d}}x}}\ln x={\frac {1}{x}} d d x log a x = 1 x ln a {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\log _{a}x={\frac {1}{x\ln a}}} {\frac {{\mathrm {d}}}{{\mathrm {d}}x}}\log _{{a}}x={\frac {1}{x\ln a}}

Memorize basic trigonometric derivatives and how to derive them. d d x sin x = cos x {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\sin x=\cos x} {\frac {{\mathrm {d}}}{{\mathrm {d}}x}}\sin x=\cos x d d x cos x = − sin x {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\cos x=-\sin x} {\frac {{\mathrm {d}}}{{\mathrm {d}}x}}\cos x=-\sin x d d x tan x = sec 2 x {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\tan x=\sec ^{2}x} {\frac {{\mathrm {d}}}{{\mathrm {d}}x}}\tan x=\sec ^{{2}}x d d x cot x = − csc 2 x {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\cot x=-\csc ^{2}x} {\frac {{\mathrm {d}}}{{\mathrm {d}}x}}\cot x=-\csc ^{{2}}x d d x sec x = sec x tan x {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\sec x=\sec x\tan x} {\frac {{\mathrm {d}}}{{\mathrm {d}}x}}\sec x=\sec x\tan x d d x csc x = − csc x cot x {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\csc x=-\csc x\cot x} {\frac {{\mathrm {d}}}{{\mathrm {d}}x}}\csc x=-\csc x\cot x
Using a Calculator
Press Alpha F2. This will open the “Window” key, where you’ll see lots of options. Scroll over to the FUNC tab if you aren’t there already. These instructions are for new models of the TI-84 and the TI-84 Plus. Older models may be slightly different.
Select nDeriv(. It’s the third option on the list. When you get to it, you can press “enter” to select it.
Enter your formula into the equation. When you hit the derivative option, your calculator will give you a blank equation that looks like this: ( d / d [ ] ) ( [ ] ) | x = [ ] {\displaystyle (d/d[])([])|x=[]} {\displaystyle (d/d[])([])|x=[]}. Go ahead and enter your specific numbers into the equation. For example, if you were finding the derivative of the function x 2 {\displaystyle x^{2}} x^{2} where x = 2 {\displaystyle x=2} {\displaystyle x=2}, you’d enter ( d / d x ) ( x 2 ) | x = 2 {\displaystyle (d/dx)(x^{2})|x=2} {\displaystyle (d/dx)(x^{2})|x=2}. If you have an equation plotted in the Y plots of your calculator, you can enter those into a blank field by pressing vars > Y-VARS > Function.
Hit “enter” to find the derivative. Once you have all of your numbers entered, you can select “enter” on your calculator to get your answer. It will (hopefully) give you your answer in an easy to understand whole number. For example, in the equation above, the derivative is 4.




















Comments
0 comment