How to Find the Height of a Triangle

Using Base and Area to Find Height

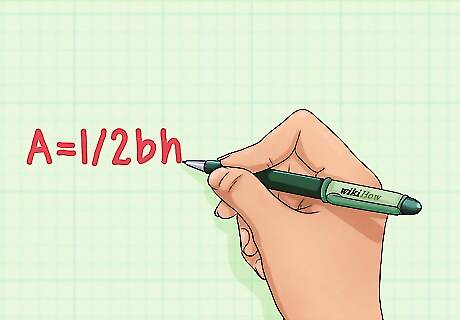
Recall the formula for the area of a triangle. The formula for the area of a triangle is A=1/2bh. A = Area of the triangle b = Length of the base of the triangle h = Height of the base of the triangle

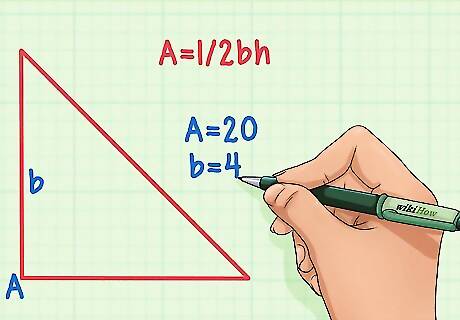
Look at your triangle and determine which variables you know. You already know the area, so assign that value to A. You should also know the value of one side length; assign that value to "'b'". Any side of a triangle can be the base, regardless of how the triangle is drawn. To visualize this, just imagine rotating the triangle until the known side length is at the bottom. ExampleIf you know that the area of a triangle is 20, and one side is 4, then:A = 20 and b = 4.

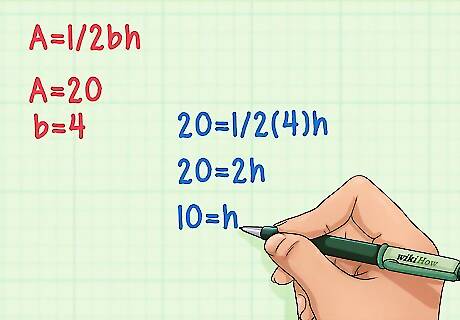
Plug your values into the equation A=1/2bh and do the math. First multiply the base (b) by 1/2, then divide the area (A) by the product. The resulting value will be the height of your triangle! Example20 = 1/2(4)h Plug the numbers into the equation.20 = 2h Multiply 4 by 1/2.10 = h Divide by 2 to find the value for height.

Finding an Equilateral Triangle's Height

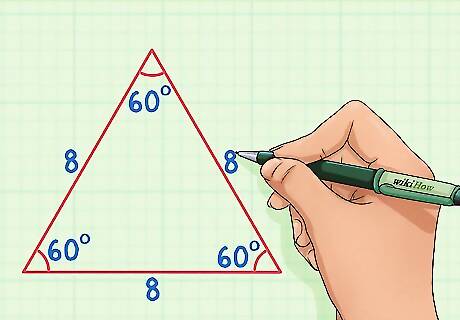
Recall the properties of an equilateral triangle. An equilateral triangle has three equal sides, and three equal angles that are each 60 degrees. If you cut an equilateral triangle in half, you will end up with two congruent right triangles. In this example, we will be using an equilateral triangle with side lengths of 8.

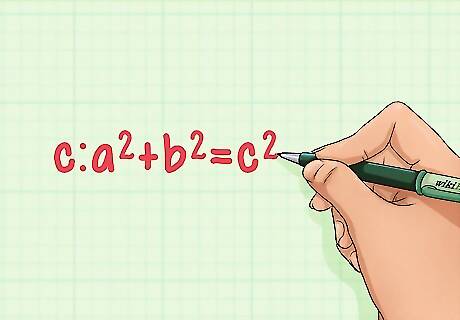
Recall the Pythagorean Theorem. The Pythagorean Theorem states that for any right triangle with sides of length a and b, and hypotenuse of length c: a + b = c. We can use this theorem to find the height of our equilateral triangle!

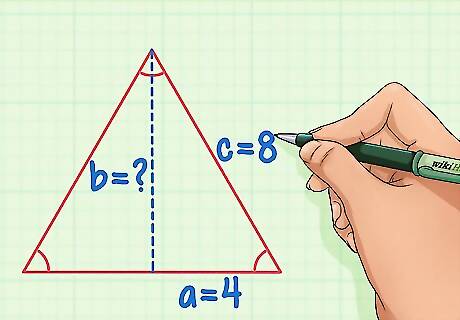
Break the equilateral triangle in half, and assign values to variables a, b, and c. The hypotenuse c will be equal to the original side length. Side a will be equal to 1/2 the side length, and side b is the height of the triangle that we need to solve. Using our example equilateral triangle with sides of 8, c = 8 and a = 4.

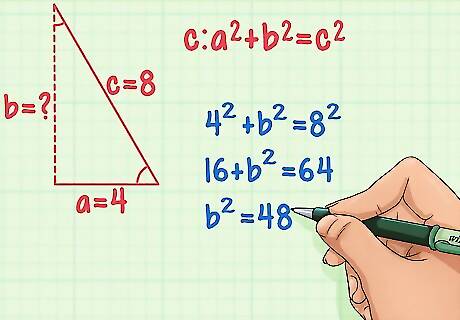
Plug the values into the Pythagorean Theorem and solve for b. First square c and a by multiplying each number by itself. Then subtract a from c. Example4 + b = 8 Plug in the values for a and c.16 + b = 64 Square a and c.b = 48 Subtract a from c.

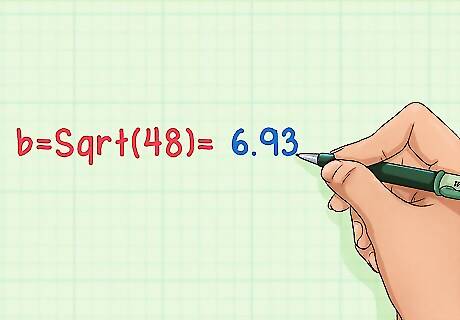
Find the square root of b to get the height of your triangle! Use the square root function on your calculator to find Sqrt(. The answer is the height of your equilateral triangle! b = Sqrt (48) = 6.93

Determining Height With Angles and Sides

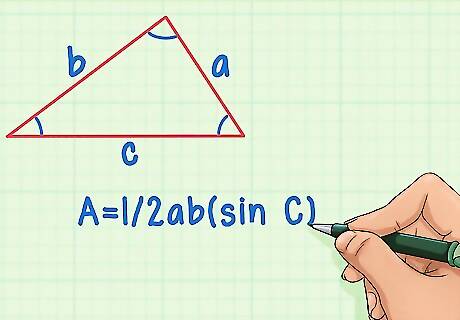
Determine what variables you know. The height of a triangle can be found if you have 2 sides and the angle in between them, or all three sides. We'll call the sides of the triangle a, b, and c, and the angles, A, B, and C. If you have all three sides, you'll use Heron's formula, and the formula for the area of a triangle. If you have two sides and an angle, you'll use the formula for the area given two angles and a side. A = 1/2ab(sin C).

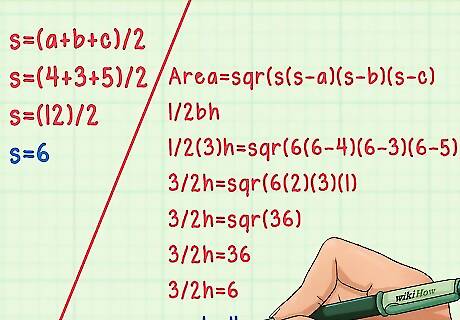
Use Heron's formula if you have all three sides. Heron's formula has two parts. First, you must find the variable s, which is equal to half of the perimeter of the triangle. This is done with this formula: s = (a+b+c)/2. Heron's Formula ExampleFor a triangle with sides a = 4, b = 3, and c = 5:s = (4+3+5)/2s = (12)/2s = 6Then use the second part of Heron's formula, Area = sqr(s(s-a)(s-b)(s-c). Replace Area in the equation with its equivalent in the area formula: 1/2bh (or 1/2ah or 1/2ch).Solve for h. For our example triangle this looks like:1/2(3)h = sqr(6(6-4)(6-3)(6-5).3/2h = sqr(6(2)(3)(1)3/2h = sqr(36)Use a calculator to calculate the square root, which in this case makes it 3/2h = 6.Therefore, height is equal to 4, using side b as the base.

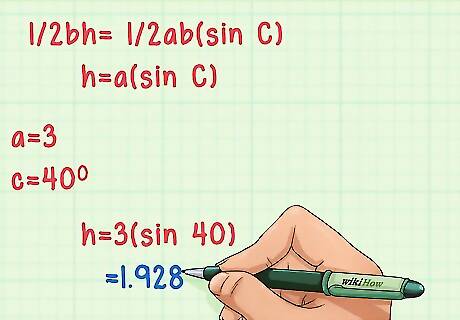
Use the area given two sides and an angle formula if you have a side and an angle. Replace area in the formula with its equivalent in the area of a triangle formula: 1/2bh. This gives you a formula that looks like 1/2bh = 1/2ab(sin C). This can be simplified to h = a(sin C), thereby eliminating one of the side variables. Note that angle C and side a are both positioned across from the height that you need to find (both on the right side from it, or both on the left side). Finding Height with 1 Side and 1 Angle ExampleFor example, with a = 3, and C = 40 degrees, the equation looks like this:h = 3(sin 40)Use your calculator to finish the equation, which makes h roughly 1.928.