views
Using a Graph of a Line
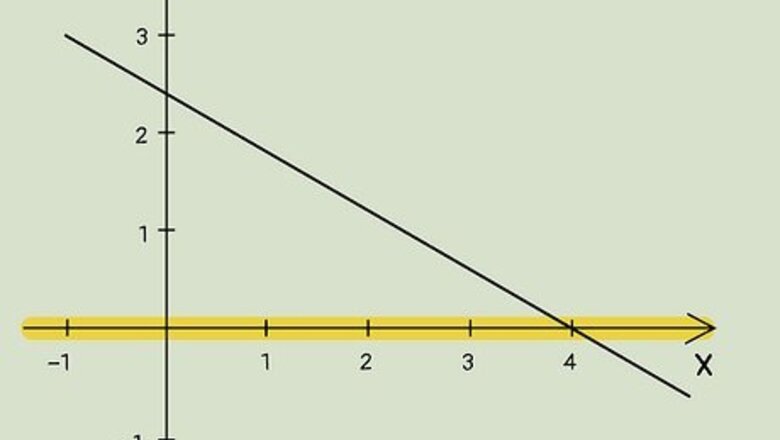
Identify the x-axis. A coordinate graph has a y-axis and an x-axis. The x-axis is the horizontal line (the line that goes from left-to-right). The y-axis is the vertical line (the line that goes up and down). It is important to look at the x-axis when locating the x-intercept.
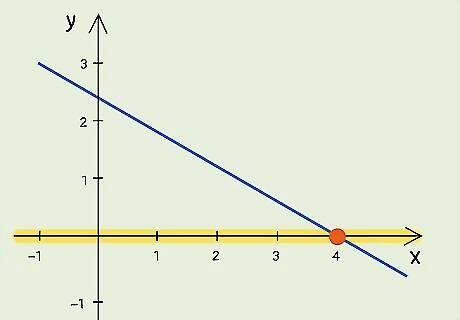
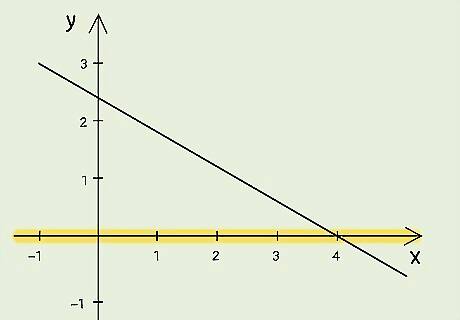
Find the point where the line crosses the x-axis. The x-intercept is this point. If you are asked to find the x-intercept based on the graph, the point will likely be exact (for example, at point 4). Usually, however, you will have to estimate using this method (for example, the point is somewhere between 4 and 5).
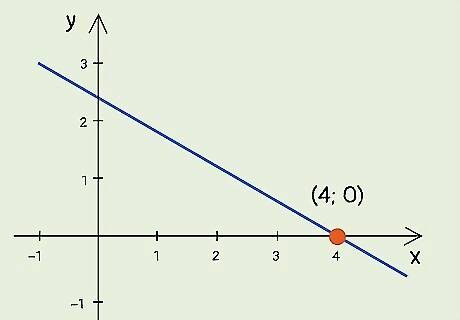
Write the ordered pair for the x-intercept. An ordered pair is written in the form ( x , y ) {\displaystyle (x,y)} (x,y) and gives you the coordinates for the point on the line. The first number of the pair is the point where the line crosses the x-axis (the x-intercept). The second number for will always be 0, since a point on the x-axis will never have a value for y. For example, if a line crosses the x-axis at point 4, the ordered pair for the x-intercept is ( 4 , 0 ) {\displaystyle (4,0)} (4,0).
Using the Equation of the Line
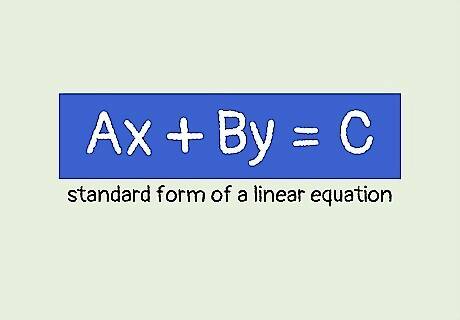
Determine that the equation of the line is in standard form. The standard form of a linear equation is A x + B y = C {\displaystyle Ax+By=C} Ax+By=C. In this form, A {\displaystyle A} A, B {\displaystyle B} B, and C {\displaystyle C} C are integers, and x {\displaystyle x} x and y {\displaystyle y} y are the coordinates of a point on the line. For example, you might be given the equation 2 x + 3 y = 6 {\displaystyle 2x+3y=6} 2x+3y=6.
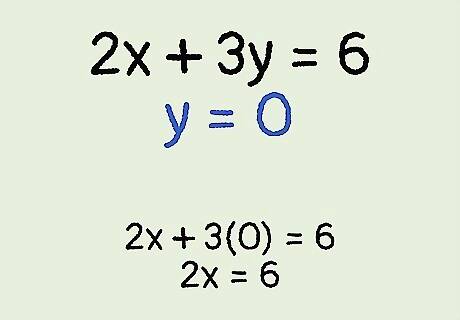
Plug in 0 for y {\displaystyle y} y. The x-intercept is the point on the line where the line crosses the x-axis. At this point, the value for y {\displaystyle y} y will be 0. So, in order to find the x-intercept, you need to set the y {\displaystyle y} y to 0 and solve for x {\displaystyle x} x. For example, if you substitute 0 for y {\displaystyle y} y, your equation will look like this: 2 x + 3 ( 0 ) = 6 {\displaystyle 2x+3(0)=6} 2x+3(0)=6, which simplifies to 2 x = 6 {\displaystyle 2x=6} 2x=6.
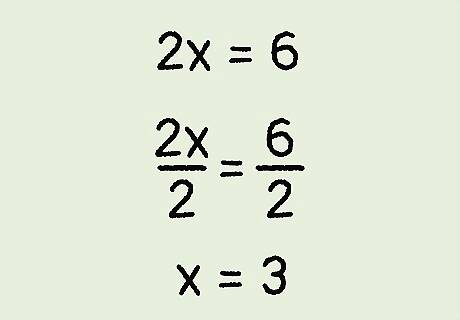
Solve for x {\displaystyle x} x. To do this, you need to isolate the x variable by dividing both sides of the equation by the coefficient. This will give you the value of x {\displaystyle x} x when y = 0 {\displaystyle y=0} y=0, which is the x-intercept. For example: 2 x = 6 {\displaystyle 2x=6} 2x=6 2 x 2 = 6 2 {\displaystyle {\frac {2x}{2}}={\frac {6}{2}}} {\frac {2x}{2}}={\frac {6}{2}} x = 3 {\displaystyle x=3} x=3
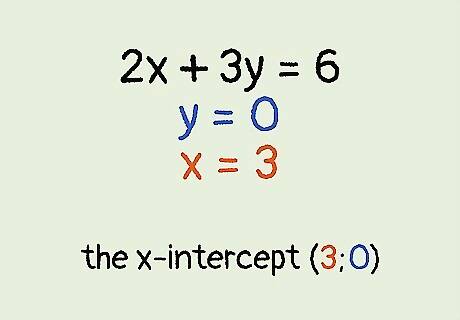
Write the ordered pair. Remember that an ordered pair is written in the form ( x , y ) {\displaystyle (x,y)} (x,y). For the x-intercept, the value of x {\displaystyle x} x will be the value you calculated previously, and the y {\displaystyle y} y value will be 0, since y {\displaystyle y} y always equals 0 at the x-intercept. For example, for the line 2 x + 3 y = 6 {\displaystyle 2x+3y=6} 2x+3y=6, the x-intercept is at the point ( 3 , 0 ) {\displaystyle (3,0)} (3,0).
Using the Quadratic Formula
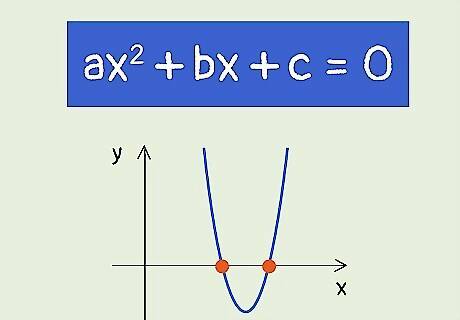
Determine that the equation of the line is a quadratic equation. A quadratic equation is an equation that takes the form a x 2 + b x + c = 0 {\displaystyle ax^{2}+bx+c=0} ax^{{2}}+bx+c=0. A quadratic equation has two solutions, which means a line written in this form is a parabola and will have two x-intercepts. For example, the equation x 2 + 3 x − 10 = 0 {\displaystyle x^{2}+3x-10=0} x^{{2}}+3x-10=0 is a quadratic equation, so this line will have two x-intercepts.
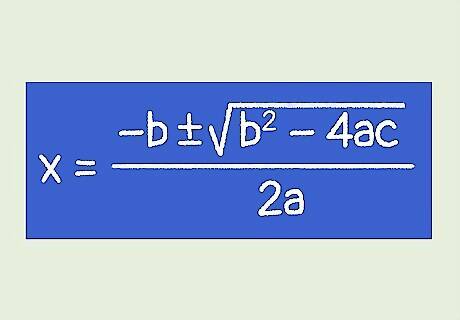
Set up the quadratic formula. The formula is x = − b ± b 2 − 4 a c 2 a {\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}} x={\frac {-b\pm {\sqrt {b^{{2}}-4ac}}}{2a}}, where a {\displaystyle a} a equals the coefficient of the second-degree term ( x 2 {\displaystyle x^{2}} x^{{2}}), b {\displaystyle b} b equals the coefficient of the first-degree term ( x {\displaystyle x} x), and c {\displaystyle c} c equals the constant.
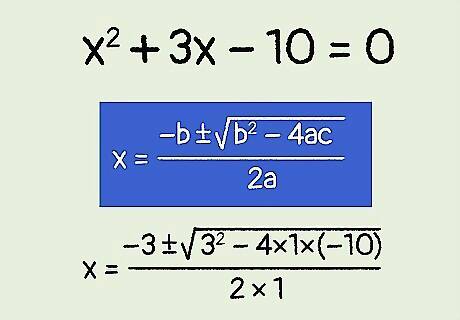
Plug all of the values into the quadratic formula. Make sure you substitute the correct values for each variable from the equation of the line. For example, if the equation of your line is x 2 + 3 x − 10 = 0 {\displaystyle x^{2}+3x-10=0} x^{{2}}+3x-10=0, your quadratic formula will look like this: x = − 3 ± 3 2 − 4 ( 1 ) ( − 10 ) 2 ( 1 ) {\displaystyle x={\frac {-3\pm {\sqrt {3^{2}-4(1)(-10)}}}{2(1)}}} x={\frac {-3\pm {\sqrt {3^{{2}}-4(1)(-10)}}}{2(1)}}.
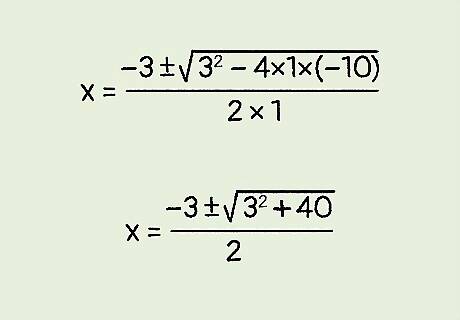
Simplify the equation. To do this, first complete all of the multiplication. Make sure you pay close attention to all positive and negative signs. For example: x = − 3 ± 3 2 − 4 ( − 10 ) 2 ( 1 ) {\displaystyle x={\frac {-3\pm {\sqrt {3^{2}-4(-10)}}}{2(1)}}} x={\frac {-3\pm {\sqrt {3^{{2}}-4(-10)}}}{2(1)}} x = − 3 ± 3 2 + 40 2 {\displaystyle x={\frac {-3\pm {\sqrt {3^{2}+40}}}{2}}} x={\frac {-3\pm {\sqrt {3^{{2}}+40}}}{2}}
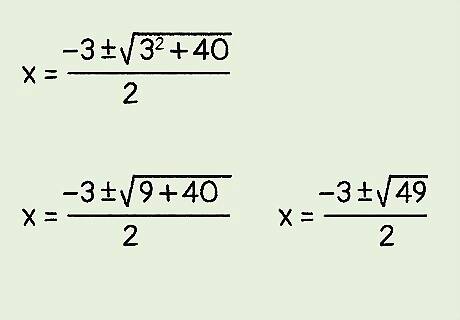
Calculate the exponent. Square the b {\displaystyle b} b term. Then, add this number to the other number under the square root sign. For example: x = − 3 ± 3 2 + 40 2 {\displaystyle x={\frac {-3\pm {\sqrt {3^{2}+40}}}{2}}} x={\frac {-3\pm {\sqrt {3^{{2}}+40}}}{2}} x = − 3 ± 9 + 40 2 {\displaystyle x={\frac {-3\pm {\sqrt {9+40}}}{2}}} x={\frac {-3\pm {\sqrt {9+40}}}{2}} x = − 3 ± 49 2 {\displaystyle x={\frac {-3\pm {\sqrt {49}}}{2}}} x={\frac {-3\pm {\sqrt {49}}}{2}}
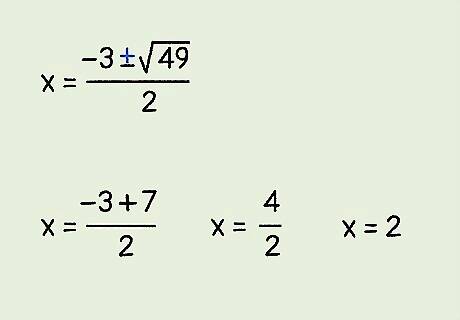
Solve for the addition formula. Since the quadratic formula has a ± {\displaystyle \pm } \pm , you will solve once by adding, and once by subtracting. Solving by adding will give you your first x {\displaystyle x} x value. For example: x = − 3 + 49 2 {\displaystyle x={\frac {-3+{\sqrt {49}}}{2}}} x={\frac {-3+{\sqrt {49}}}{2}} x = − 3 + 7 2 {\displaystyle x={\frac {-3+7}{2}}} x={\frac {-3+7}{2}} x = 4 2 {\displaystyle x={\frac {4}{2}}} x={\frac {4}{2}} x = 2 {\displaystyle x=2} x=2
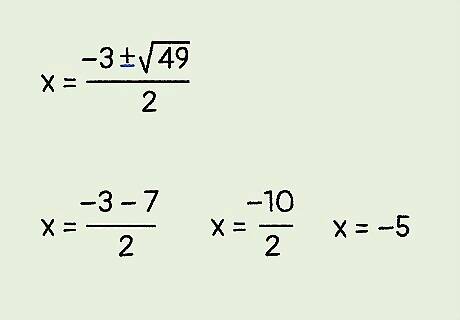
Solve for the subtraction formula. This will give you the second value for x {\displaystyle x} x. First calculate the square root, then find the difference in the numerator. Finally, divide by 2. For example: x = − 3 − 49 2 {\displaystyle x={\frac {-3-{\sqrt {49}}}{2}}} x={\frac {-3-{\sqrt {49}}}{2}} x = − 3 − 7 2 {\displaystyle x={\frac {-3-7}{2}}} x={\frac {-3-7}{2}} x = − 10 2 {\displaystyle x={\frac {-10}{2}}} x={\frac {-10}{2}} x = − 5 {\displaystyle x=-5} x=-5

Find the ordered pairs for the x-intercept. Remember that an ordered pair gives the x-coordinate first, then the y-coordinate ( x , y ) {\displaystyle (x,y)} (x,y). The x {\displaystyle x} x values will be the values you calculated using the quadratic formula. The y {\displaystyle y} y value will be 0, since at the x-intercept, y {\displaystyle y} y always equals 0. For example, for the line x 2 + 3 x − 10 = 0 {\displaystyle x^{2}+3x-10=0} x^{{2}}+3x-10=0, the x-intercepts are at points ( 2 , 0 ) {\displaystyle (2,0)} (2,0) and ( − 5 , 0 ) {\displaystyle (-5,0)} (-5,0).



















Comments
0 comment