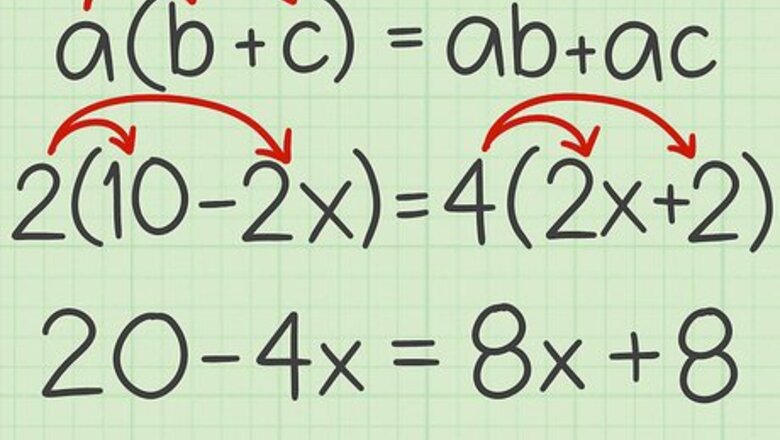
views
Solving Equations with One Variable on Both Sides
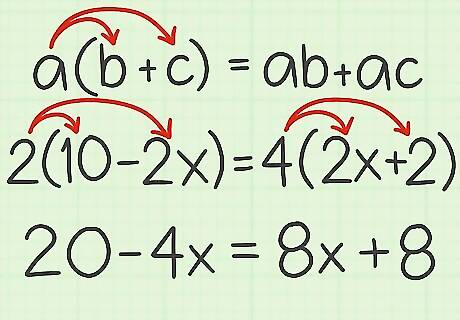
Apply the distributive property, if necessary. The distributive property states that a ( b + c ) = a b + a c {\displaystyle a(b+c)=ab+ac} a(b+c)=ab+ac. This rule allows you to cancel out parentheses by multiplying each term in the parentheses by the number outside the parentheses. For example, if your equation is 2 ( 10 − 2 x ) = 4 ( 2 x + 2 ) {\displaystyle 2(10-2x)=4(2x+2)} 2(10-2x)=4(2x+2), use the distributive property to multiply the terms in parentheses by the number outside the parentheses: 2 ( 10 − 2 x ) = 4 ( 2 x + 2 ) {\displaystyle 2(10-2x)=4(2x+2)} 2(10-2x)=4(2x+2) 20 − 4 x = 8 x + 8 {\displaystyle 20-4x=8x+8} 20-4x=8x+8
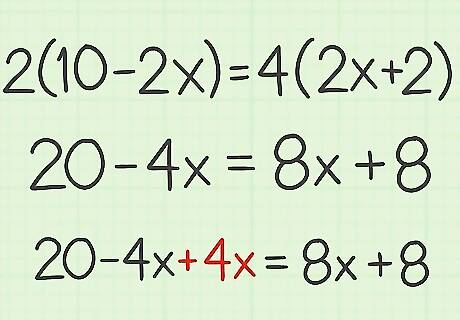
Cancel the variable on one side of the equation. To cancel the variable, complete the opposite operation as stated in the equation. For example, if the term is subtracted in the equation, cancel it by adding. If the term is added in the equation, cancel it by subtracting. It is usually easiest to cancel the variable with the smaller coefficient. For example, in the equation 20 − 4 x = 8 x + 8 {\displaystyle 20-4x=8x+8} 20-4x=8x+8, cancel the term − 4 x {\displaystyle -4x} -4x by adding 4 x {\displaystyle 4x} 4x: 20 − 4 x + 4 x = 8 x + 8 {\displaystyle 20-4x+4x=8x+8} 20-4x+4x=8x+8.
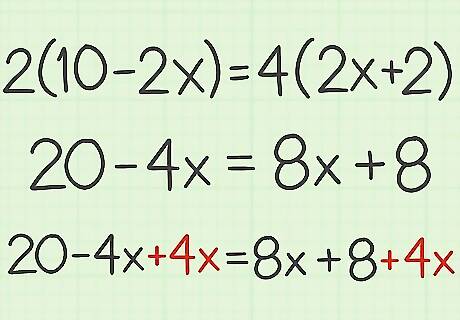
Keep the equation balanced. Whatever you do to one side of the equation, you must do to the other side as well. So if you add or subtract to cancel the variable on one side of the equation, you must add or subtract to the other side as well. For example, if you added 4 x {\displaystyle 4x} 4x on one side of the equation to cancel the variable, you must also add 4 x {\displaystyle 4x} 4x to the other side of the equation: 20 − 4 x + 4 x = 8 x + 8 + 4 x {\displaystyle 20-4x+4x=8x+8+4x} 20-4x+4x=8x+8+4x
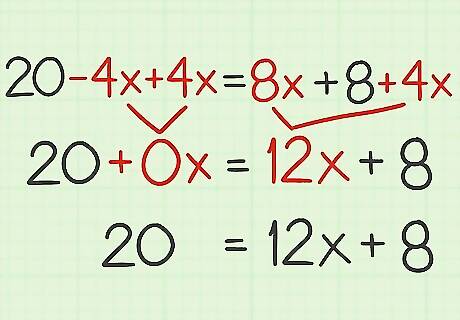
Simplify the equation by combining like terms. You should now have the variable on one side of the equation. For example: 20 − 4 x + 4 x = 8 x + 8 + 4 x {\displaystyle 20-4x+4x=8x+8+4x} 20-4x+4x=8x+8+4x 20 = 12 x + 8 {\displaystyle 20=12x+8} 20=12x+8
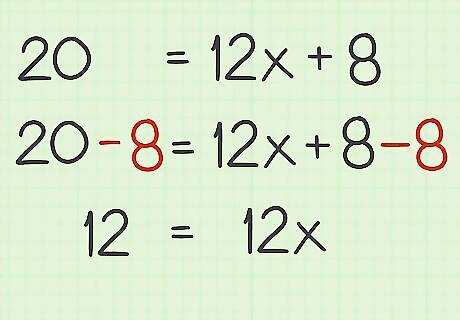
Move the constants to one side of the equation, if necessary. You want the variable term on one side, and the constant on the other side. To move the constant to one side, add or subtract from each side of the equation to cancel the term on one side. For example, to cancel the + 8 {\displaystyle +8} +8 constant on the variable side, subtract 8 from both sides of the equation: 20 = 12 x + 8 {\displaystyle 20=12x+8} 20=12x+8 20 − 8 = 12 x + 8 − 8 {\displaystyle 20-8=12x+8-8} 20-8=12x+8-8 12 = 12 x {\displaystyle 12=12x} 12=12x
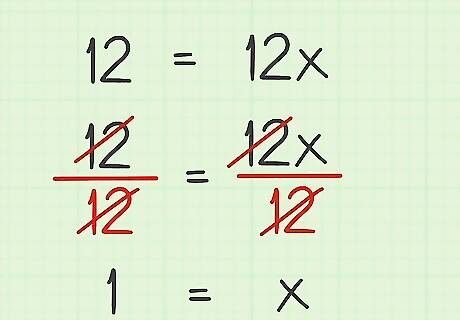
Cancel the variable’s coefficient. To do this, perform the operation opposite from the one denoted in the equation. Usually this will mean dividing to cancel a coefficient being multiplied by a variable. Remember that whatever you do to one side of the equation, you must do to the other side of the equation as well. For example, to cancel out the coefficient 12 from the equation, you would divide each side of the equation by 12: 12 = 12 x {\displaystyle 12=12x} 12=12x 12 12 = 12 x 12 {\displaystyle {\frac {12}{12}}={\frac {12x}{12}}} {\frac {12}{12}}={\frac {12x}{12}} 1 = x {\displaystyle 1=x} 1=x
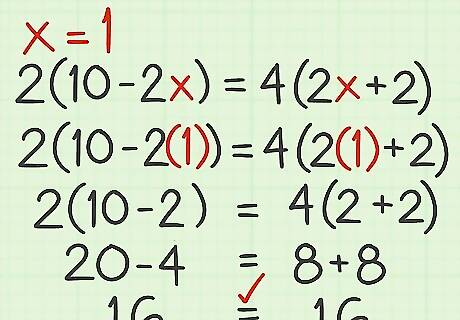
Check your work. To make sure your answer is correct, substitute your solution back into the original equation. If the equation is true, your answer is correct. For example, if 1 = x {\displaystyle 1=x} 1=x, substitute 1 for the variable in the equation and calculate: 2 ( 10 − 2 x ) = 4 ( 2 x + 2 ) {\displaystyle 2(10-2x)=4(2x+2)} 2(10-2x)=4(2x+2) 2 ( 10 − 2 ( 1 ) ) = 4 ( 2 ( 1 ) + 2 ) {\displaystyle 2(10-2(1))=4(2(1)+2)} 2(10-2(1))=4(2(1)+2) 2 ( 10 − 2 ) = 4 ( 2 + 2 ) {\displaystyle 2(10-2)=4(2+2)} 2(10-2)=4(2+2) 20 − 4 = 8 + 8 {\displaystyle 20-4=8+8} 20-4=8+8 16 = 16 {\displaystyle 16=16} 16=16
Solving System Equations with Two Variables
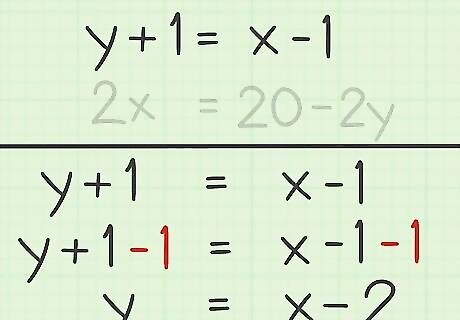
Isolate a variable in one equation. This might already be done. If not, use the rules of algebra to isolate the variable on one side of the equation. Remember that whatever you do to one side of the equation, you must do to the other side. For example, for the equation y + 1 = x − 1 {\displaystyle y+1=x-1} y+1=x-1, to isolate the y {\displaystyle y} y variable, you would subtract 1 from both sides: y + 1 = x − 1 {\displaystyle y+1=x-1} y+1=x-1 y + 1 − 1 = x − 1 − 1 {\displaystyle y+1-1=x-1-1} y+1-1=x-1-1 y = x − 2 {\displaystyle y=x-2} y=x-2 EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher To solve an equation for a variable like "x," you need to manipulate the equation to isolate x. Use techniques like the distributive property, combining like terms, factoring, adding or subtracting the same number, and multiplying or dividing by the same non-zero number to isolate "x" and find the answer.
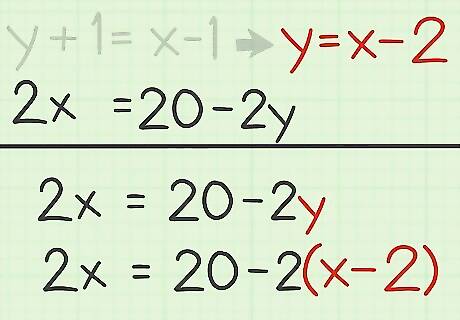
Substitute the value of the isolated variable into the other equation. Make sure you substitute the entire expression for the variable. This will give you an equation with only one variable, allowing you to solve for the variable. For example, if your first equation is 2 x = 20 − 2 y {\displaystyle 2x=20-2y} 2x=20-2y, and you determined y = x − 2 {\displaystyle y=x-2} y=x-2 in the second equation, you would substitute x − 2 {\displaystyle x-2} x-2 for y {\displaystyle y} y in the first equation: 2 x = 20 − 2 y {\displaystyle 2x=20-2y} 2x=20-2y 2 x = 20 − 2 ( x − 2 ) {\displaystyle 2x=20-2(x-2)} 2x=20-2(x-2)
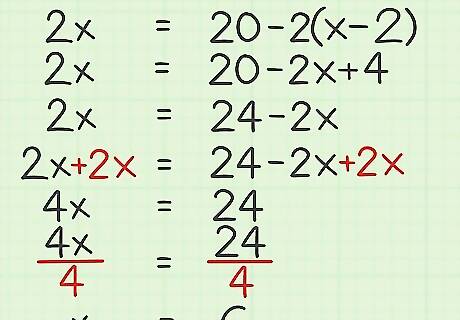
Solve for the variable. To do this, move the variable to one side of the equation. Then, move the constants to one side of the equation. Then, isolate the variable using multiplication or division. For example: 2 x = 20 − 2 ( x − 2 ) {\displaystyle 2x=20-2(x-2)} 2x=20-2(x-2) 2 x = 20 − 2 x + 4 {\displaystyle 2x=20-2x+4} 2x=20-2x+4 2 x = 24 − 2 x {\displaystyle 2x=24-2x} 2x=24-2x 2 x + 2 x = 24 − 2 x + 2 x {\displaystyle 2x+2x=24-2x+2x} 2x+2x=24-2x+2x 4 x = 24 {\displaystyle 4x=24} 4x=24 4 x 4 = 24 4 {\displaystyle {\frac {4x}{4}}={\frac {24}{4}}} {\frac {4x}{4}}={\frac {24}{4}} x = 6 {\displaystyle x=6} x=6
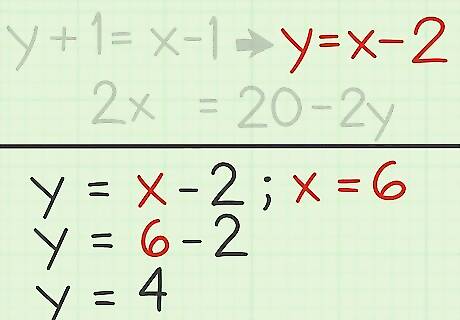
Solve for the remaining variable. To do this, plug the value of the variable you already solved into one of the equations. This will give you an equation with only one variable. Solve for the variable using the rules of algebra. You can use either equation to solve for the remaining variable. For example, if you found that x = 6 {\displaystyle x=6} x=6, you can substitute 6 for x {\displaystyle x} x in the second equation: y = x − 2 {\displaystyle y=x-2} y=x-2 y = ( 6 ) − 2 {\displaystyle y=(6)-2} y=(6)-2 y = 4 {\displaystyle y=4} y=4
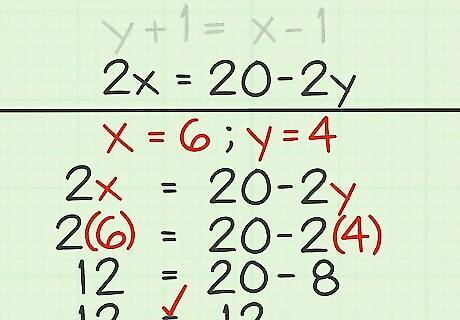
Check your work. Plug the values for both variables into one of the equations. If the equation is true, your solutions are correct. For example, if you found that x = 6 {\displaystyle x=6} x=6 and y = 4 {\displaystyle y=4} y=4, plug these back into the original equation and solve: 2 x = 20 − 2 y {\displaystyle 2x=20-2y} 2x=20-2y 2 ( 6 ) = 20 − 2 ( 4 ) {\displaystyle 2(6)=20-2(4)} 2(6)=20-2(4) 12 = 20 − 8 {\displaystyle 12=20-8} 12=20-8 12 = 12 {\displaystyle 12=12} 12=12
Solving Example Problems
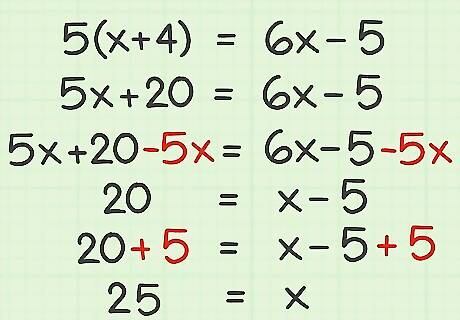
Try this problem using the distributive property with one variable: 5 ( x + 4 ) = 6 x − 5 {\displaystyle 5(x+4)=6x-5} 5(x+4)=6x-5. Use the distributive property to cancel the parentheses: 5 ( x + 4 ) = 6 x − 5 {\displaystyle 5(x+4)=6x-5} 5(x+4)=6x-5 5 x + 20 = 6 x − 5 {\displaystyle 5x+20=6x-5} 5x+20=6x-5 Cancel the 5 x {\displaystyle 5x} 5x on the left side of the equation by subtracting 5 x {\displaystyle 5x} 5x from both sides: 5 x + 20 = 6 x − 5 {\displaystyle 5x+20=6x-5} 5x+20=6x-5 5 x + 20 − 5 x = 6 x − 5 − 5 x {\displaystyle 5x+20-5x=6x-5-5x} 5x+20-5x=6x-5-5x 20 = x − 5 {\displaystyle 20=x-5} 20=x-5 Isolate the variable by adding 5 to each side of the equation: 20 = x − 5 {\displaystyle 20=x-5} 20=x-5 20 + 5 = x − 5 + 5 {\displaystyle 20+5=x-5+5} 20+5=x-5+5 25 = x {\displaystyle 25=x} 25=x EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher The distributive property helps you avoid repetitive calculations. You can use the distributive property to solve equations where you must multiply a number by a sum or difference. It simplifies calculations, enables expression manipulation (like factoring), and forms the basis for solving many equations.
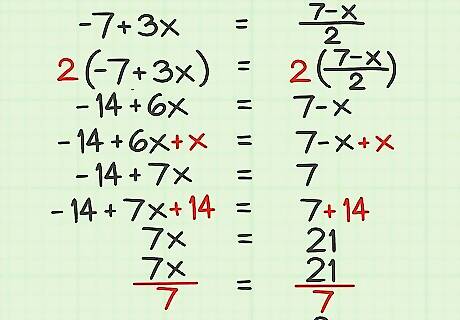
Try this problem involving a fraction: − 7 + 3 x = 7 − x 2 {\displaystyle -7+3x={\frac {7-x}{2}}} -7+3x={\frac {7-x}{2}}. Remove the fraction. To do this, multiply each side of the equation by the fraction’s denominator: − 7 + 3 x = 7 − x 2 {\displaystyle -7+3x={\frac {7-x}{2}}} -7+3x={\frac {7-x}{2}} 2 ( − 7 + 3 x ) = 2 ( 7 − x 2 ) {\displaystyle 2(-7+3x)=2({\frac {7-x}{2}})} 2(-7+3x)=2({\frac {7-x}{2}}) − 14 + 6 x = 7 − x {\displaystyle -14+6x=7-x} -14+6x=7-x Cancel the − x {\displaystyle -x} -x on the right side of the equation by adding x {\displaystyle x} x to each side of the equation: − 14 + 6 x = 7 − x {\displaystyle -14+6x=7-x} -14+6x=7-x − 14 + 6 x + x = 7 − x + x {\displaystyle -14+6x+x=7-x+x} -14+6x+x=7-x+x − 14 + 7 x = 7 {\displaystyle -14+7x=7} -14+7x=7 Move the constants to one side of the equation by adding 14 to each side: − 14 + 7 x = 7 {\displaystyle -14+7x=7} -14+7x=7 − 14 + 7 x + 14 = 7 + 14 {\displaystyle -14+7x+14=7+14} -14+7x+14=7+14 7 x = 21 {\displaystyle 7x=21} 7x=21 Cancel the coefficient by dividing each side of the equation by 7: 7 x = 21 {\displaystyle 7x=21} 7x=21 7 x 7 = 21 7 {\displaystyle {\frac {7x}{7}}={\frac {21}{7}}} {\frac {7x}{7}}={\frac {21}{7}} x = 3 {\displaystyle x=3} x=3
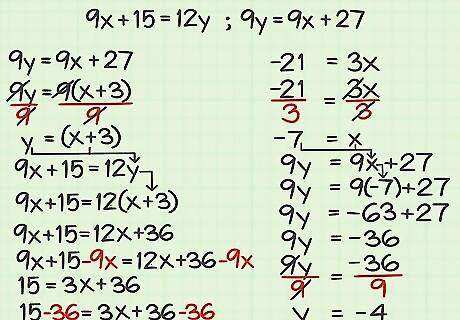
Try solving this system of equations: 9 x + 15 = 12 y ; 9 y = 9 x + 27 {\displaystyle 9x+15=12y;9y=9x+27} 9x+15=12y;9y=9x+27 Isolate the y {\displaystyle y} y variable in the second equation: 9 y = 9 x + 27 {\displaystyle 9y=9x+27} 9y=9x+27 9 y = 9 ( x + 3 ) {\displaystyle 9y=9(x+3)} 9y=9(x+3) 9 y 9 = 9 ( x + 3 ) 9 {\displaystyle {\frac {9y}{9}}={\frac {9(x+3)}{9}}} {\frac {9y}{9}}={\frac {9(x+3)}{9}} y = x + 3 {\displaystyle y=x+3} y=x+3 Plug in x + 3 {\displaystyle x+3} x+3 for y {\displaystyle y} y in the first equation: 9 x + 15 = 12 y {\displaystyle 9x+15=12y} 9x+15=12y 9 x + 15 = 12 ( x + 3 ) {\displaystyle 9x+15=12(x+3)} 9x+15=12(x+3) Use the distributive property to cancel the parentheses: 9 x + 15 = 12 x + 36 {\displaystyle 9x+15=12x+36} 9x+15=12x+36 Cancel the variable on the left side of the equation by subtracting 9 x {\displaystyle 9x} 9x from each side: 9 x + 15 = 12 x + 36 {\displaystyle 9x+15=12x+36} 9x+15=12x+36 9 x + 15 − 9 x = 12 x + 36 − 9 x {\displaystyle 9x+15-9x=12x+36-9x} 9x+15-9x=12x+36-9x 15 = 3 x + 36 {\displaystyle 15=3x+36} 15=3x+36 Move the constants to one side by subtracting 36 from each side: 15 = 3 x + 36 {\displaystyle 15=3x+36} 15=3x+36 15 − 36 = 3 x + 36 − 36 {\displaystyle 15-36=3x+36-36} 15-36=3x+36-36 − 21 = 3 x {\displaystyle -21=3x} -21=3x Cancel the coefficient by dividing each side by 3: − 21 = 3 x {\displaystyle -21=3x} -21=3x − 21 3 = 3 x 3 {\displaystyle {\frac {-21}{3}}={\frac {3x}{3}}} {\frac {-21}{3}}={\frac {3x}{3}} − 7 = x {\displaystyle -7=x} -7=x Solve for y {\displaystyle y} y by plugging the value of x {\displaystyle x} x into either equation: 9 y = 9 x + 27 {\displaystyle 9y=9x+27} 9y=9x+27 9 y = 9 ( − 7 ) + 27 {\displaystyle 9y=9(-7)+27} 9y=9(-7)+27 9 y = − 63 + 27 {\displaystyle 9y=-63+27} 9y=-63+27 9 y = − 36 {\displaystyle 9y=-36} 9y=-36 9 y 9 = − 36 9 {\displaystyle {\frac {9y}{9}}={\frac {-36}{9}}} {\frac {9y}{9}}={\frac {-36}{9}} y = − 4 {\displaystyle y=-4} y=-4



















Comments
0 comment