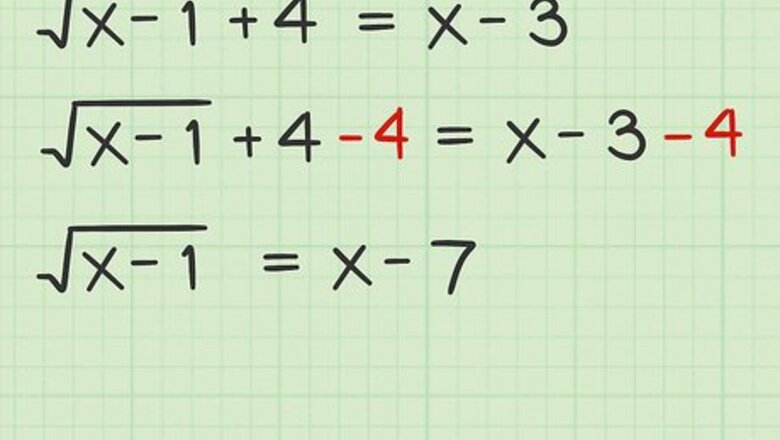
views
{\displaystyle {\sqrt {}}}
symbol, so the problem is called a “radical equation.”[1]
X
Research source
To solve a radical equation, you have to eliminate the root by isolating it, squaring or cubing the equation, and then simplifying to find your answer. However, this procedure can create answers that appear to be correct, but are not, because of the squaring process. These are called extraneous solutions. You must learn to identify and discard the extraneous solutions.
Removing the Radical
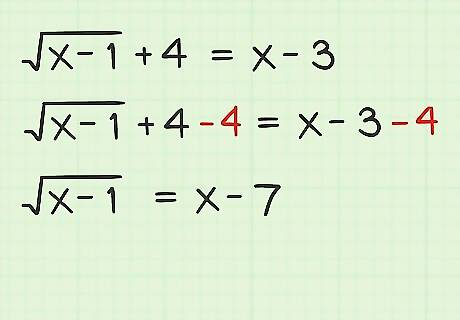
Isolate the radical term. The first step to solving a radical equation is to move the radical term to stand alone on one side of the equation. Move all other terms to the opposite side. In this step, if possible, combine any other like terms that may exist. Consider the sample problem x − 1 + 4 = x − 3 {\displaystyle {\sqrt {x-1}}+4=x-3} {\sqrt {x-1}}+4=x-3. Your first step is to isolate the radical on the left side of the equation, as follows: x − 1 + 4 = x − 3 {\displaystyle {\sqrt {x-1}}+4=x-3} {\sqrt {x-1}}+4=x-3 x − 1 + 4 − 4 = x − 3 − 4 {\displaystyle {\sqrt {x-1}}+4-4=x-3-4} {\sqrt {x-1}}+4-4=x-3-4 ………. (subtract 4 from both sides) x − 1 = x − 7 {\displaystyle {\sqrt {x-1}}=x-7} {\sqrt {x-1}}=x-7 ………. (combine like terms)
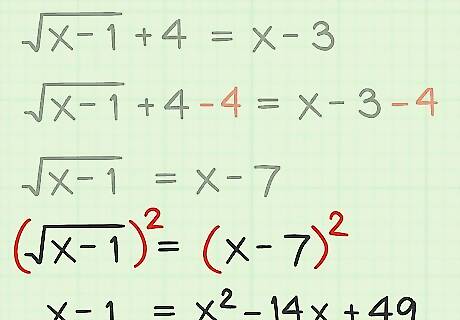
Square both sides of the equation. To remove the radical sign from the problem, you need to perform its opposite function. The opposite of the square root function is to square both sides of the equation. Be careful, when squaring both sides of the equation, to do so correctly. Recall, for example, that ( x − 7 ) 2 {\displaystyle (x-7)^{2}} (x-7)^{2} is NOT x 2 − 7 2 {\displaystyle x^{2}-7^{2}} x^{2}-7^{2}. You need to treat the ( x − 7 ) {\displaystyle (x-7)} (x-7) term as a binomial and square it accordingly. Continue working with the sample problem and square both sides of it as follows: x − 1 = x − 7 {\displaystyle {\sqrt {x-1}}=x-7} {\sqrt {x-1}}=x-7 ( x − 1 ) 2 = ( x − 7 ) 2 {\displaystyle ({\sqrt {x-1}})^{2}=(x-7)^{2}} ({\sqrt {x-1}})^{2}=(x-7)^{2} x − 1 = x 2 − 14 x + 49 {\displaystyle x-1=x^{2}-14x+49} x-1=x^{2}-14x+49 If you need help with this step, you may want to review Multiply Binomials.
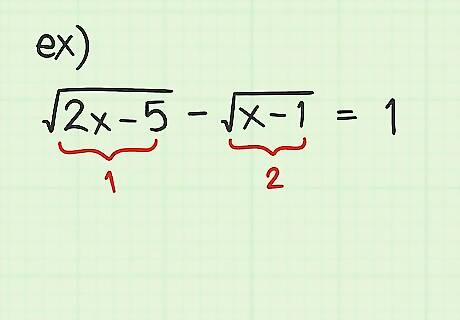
Repeat the previous steps if necessary. If your original problem contained two or more radical terms, then the first round of isolating and squaring may not have removed all the radicals. If that is the case, then you should, once again, manipulate your equation to isolate the radical that remains and square each side again. An example of such a problem would be something like 2 x − 5 − x − 1 = 1 {\displaystyle {\sqrt {2x-5}}-{\sqrt {x-1}}=1} {\sqrt {2x-5}}-{\sqrt {x-1}}=1. Because of the two radicals, you will need to do this procedure twice.
Finding all Possible Solutions
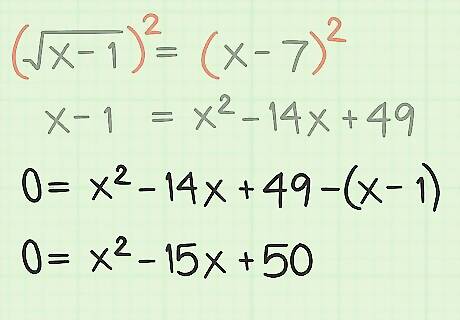
Consolidate and combine like terms. After you have eliminated all the radicals from the problem, move all the terms to one side of the equation and combine like terms. Returning to the working sample problem, this looks as follows: x − 1 = x 2 − 14 x + 49 {\displaystyle x-1=x^{2}-14x+49} x-1=x^{2}-14x+49 0 = x 2 − 15 x + 50 {\displaystyle 0=x^{2}-15x+50} 0=x^{2}-15x+50
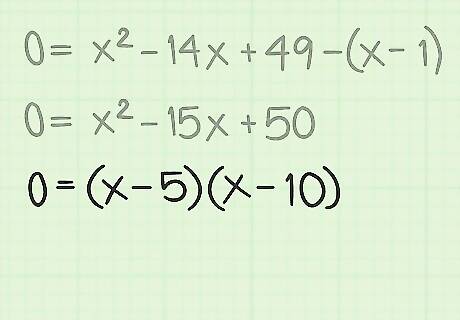
Solve the equation. In most cases, this step will create a quadratic polynomial. This is an equation that contains an x 2 {\displaystyle x^{2}} x^{2} term as its highest variable. If the original radical was something other than a square root (such as a cube root or fourth root, for example), then you may have a more difficult problem. We will focus on the quadratic for this article. You may be able to solve the quadratic equation by factoring, or you can go directly to the quadratic formula. In this case, the sample problem, 0 = x 2 − 15 x + 50 {\displaystyle 0=x^{2}-15x+50} 0=x^{2}-15x+50, can be factored into the two binomial factors of ( x − 5 ) {\displaystyle (x-5)} (x-5) and ( x − 10 ) {\displaystyle (x-10)} (x-10).
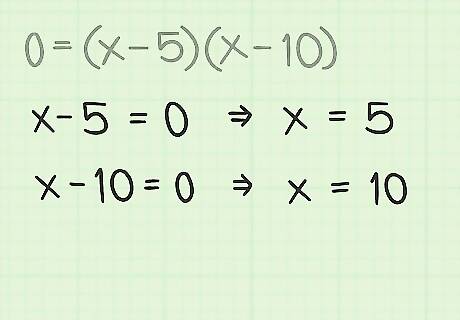
Determine your solutions. Factoring the quadratic equation in this case suggests two possible solutions. Because the quadratic equation is equal to 0, you find the solutions by setting each factor equal to 0 and then solve. In the working problem, the two factors are ( x − 5 ) {\displaystyle (x-5)} (x-5) and ( x − 10 ) {\displaystyle (x-10)} (x-10). Set each of these equal to 0 to get the solutions x = 5 {\displaystyle x=5} x=5 and x = 10 {\displaystyle x=10} x=10. With another problem, you may not be able to factor and would then have to use the quadratic formula to find the solution.
Discarding the Extraneous Solutions
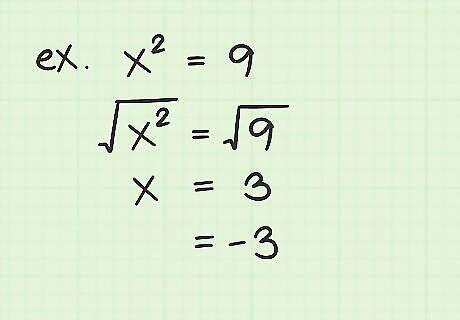
Recognize the potential for an extraneous solution. Recall that after isolating the radical on one side of the equation, you then squared both sides to remove the radical sign. This is a necessary step to solving the problem. However, the squaring operation is what creates the extraneous solutions. Remember some basic mathematics, that both a negative and a positive number, when squared, will give the same result. For example, ( − 3 ) 2 {\displaystyle (-3)^{2}} (-3)^{2} and 3 2 {\displaystyle 3^{2}} 3^{2} both give the answer of 9 {\displaystyle 9} 9. However, both the negative and positive numbers might not be solutions to whatever problem you are solving. The one that does not work is called the extraneous solution.
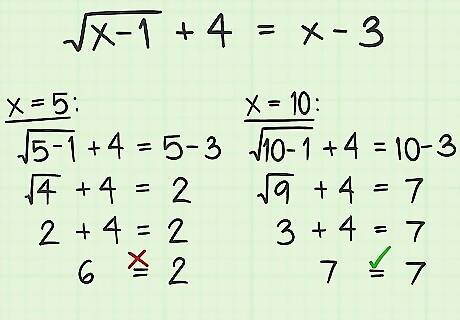
Test each of your solutions in the original problem. After you have found the solutions to your problem, you may have found one, two or more different possible values for the variable. You need to check each of these in the original problem to see which work. Remember that the original problem here was x − 1 + 4 = x − 3 {\displaystyle {\sqrt {x-1}}+4=x-3} {\sqrt {x-1}}+4=x-3. First check the solution x = 5 {\displaystyle x=5} x=5: x − 1 + 4 = x − 3 {\displaystyle {\sqrt {x-1}}+4=x-3} {\sqrt {x-1}}+4=x-3 5 − 1 + 4 = 5 − 3 {\displaystyle {\sqrt {5-1}}+4=5-3} {\sqrt {5-1}}+4=5-3 ………. (substitute 5 for x) 4 + 4 = 5 − 3 {\displaystyle {\sqrt {4}}+4=5-3} {\sqrt {4}}+4=5-3 2 + 4 = 5 − 3 {\displaystyle 2+4=5-3} 2+4=5-3 6 = 2 {\displaystyle 6=2} 6=2. Because your result is an incorrect statement, the original solution of x = 5 {\displaystyle x=5} x=5 must be an extraneous solution that was caused by the squaring process. Check the second solution x = 10 {\displaystyle x=10} x=10: x − 1 + 4 = x − 3 {\displaystyle {\sqrt {x-1}}+4=x-3} {\sqrt {x-1}}+4=x-3 10 − 1 + 4 = 10 − 3 {\displaystyle {\sqrt {10-1}}+4=10-3} {\sqrt {10-1}}+4=10-3 9 + 4 = 10 − 3 {\displaystyle {\sqrt {9}}+4=10-3} {\sqrt {9}}+4=10-3 3 + 4 = 10 − 3 {\displaystyle 3+4=10-3} 3+4=10-3 7 = 7 {\displaystyle 7=7} 7=7 In this case, you get a true statement. This shows that the solution x = 10 {\displaystyle x=10} x=10 is a true solution to the original problem.
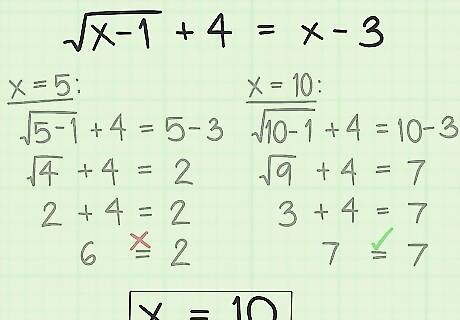
Discard the extraneous solution and report your result. The extraneous solution is incorrect and can be discarded. Whatever remains is the answer to your problem. In this case, you would report that x = 10 {\displaystyle x=10} x=10.


















Comments
0 comment