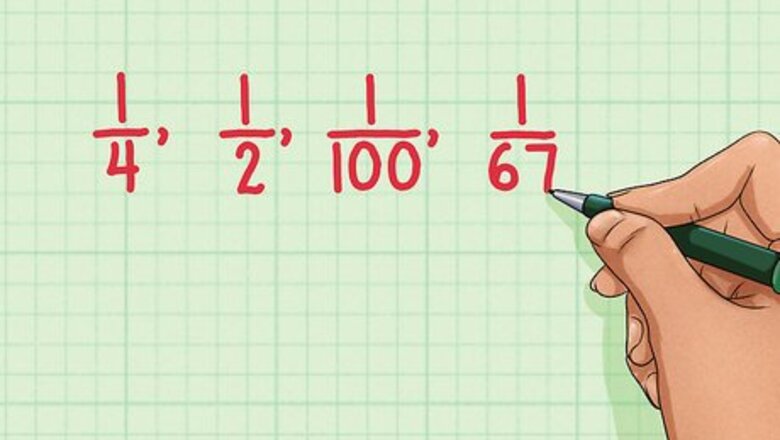
views
Identifying Reduced Fractions
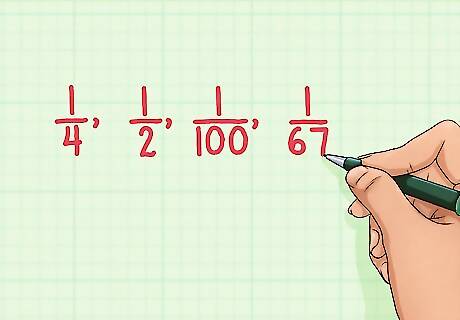
Look for unit fractions. A unit fraction is one that has 1 as the numerator. Unit fractions cannot be simplified any further. For example, 1 4 {\displaystyle {\frac {1}{4}}} {\frac {1}{4}}, 1 2 {\displaystyle {\frac {1}{2}}} {\frac {1}{2}}, 1 100 {\displaystyle {\frac {1}{100}}} {\frac {1}{100}}, and 1 67 {\displaystyle {\frac {1}{67}}} {\frac {1}{67}} are all simplified, because they have 1 as the numerator.
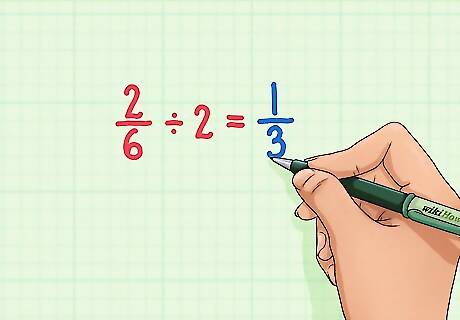
Determine whether the denominator is a multiple of the numerator. One way to reduce a fraction is to divide by a greatest common factor. If the denominator is a multiple of the numerator, that means each can be divided by a greatest common factor (the numerator). These types of fractions can be reduced to a unit fraction. For example, 2 6 {\displaystyle {\frac {2}{6}}} {\frac {2}{6}} is not simplified, because 6 is a multiple of 2. The numerator and denominator can still be divided by a common factor of 2, simplifying the fraction to 1 3 {\displaystyle {\frac {1}{3}}} {\frac {1}{3}}. The fraction 2 5 {\displaystyle {\frac {2}{5}}} {\frac {2}{5}} is simplified, because 5 is not a multiple of 2.
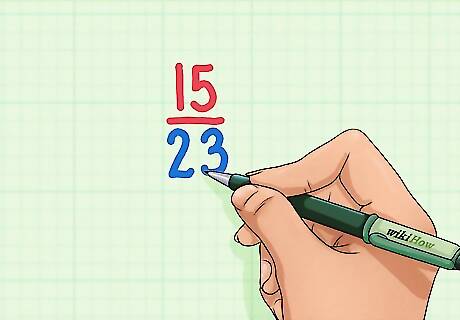
Determine whether the denominator is a prime number. A prime number is a number that is only divisible by itself and 1. If the denominator is prime, the fraction cannot be simplified any further. This is because the denominator can only be divided by itself, so whatever number appears in the numerator will not have a common factor. For more information about prime numbers, you can read Check if a Number Is Prime. For example, 15 23 {\displaystyle {\frac {15}{23}}} {\frac {15}{23}} is simplified, because 23 is a prime number. The only factors of 23 are 23 and 1, so it is impossible to find a greatest common factor you can use to simplify the numerator and denominator. (If the numerator were 1, it would be a unit fraction and thus already simplified. If the numerator were 23, the fraction would equal 1.)

Find the difference between the numerator and the denominator. If the difference is 1, then the fraction is simplified. For example, you know that 7 8 {\displaystyle {\frac {7}{8}}} {\frac {7}{8}} is simplified, because 8 − 7 = 1 {\displaystyle 8-7=1} 8-7=1
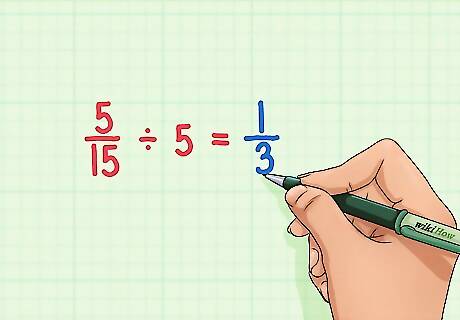
Reduce Fractions that aren't already simplified. A fraction can be simplified by looking for the largest number that can be evenly divided into the numerator and denominator, and then dividing each by that number. For example, if you are reducing 5 15 {\displaystyle {\frac {5}{15}}} {\frac {5}{15}}, divide the numerator and denominator by 5. This will give you 1 3 {\displaystyle {\frac {1}{3}}} {\frac {1}{3}}, which you know cannot be reduced further because it is a unit fraction. EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher To simplify fractions, you can divide both the numerator and denominator by a common factor. This creates a new, easier-to-use fraction with smaller components, but it represents the same value. For instance, if you divide both the numerator and denominator of 6/12 by 2, you get 3/6, which is equal to 1/2.
Using Shortcuts in Context

Determine which of the following fractions are in their reduced form. Do not make any calculations: 1 5 {\displaystyle {\frac {1}{5}}} {\frac {1}{5}}, 1 10 {\displaystyle {\frac {1}{10}}} {\frac {1}{10}}, 5 10 {\displaystyle {\frac {5}{10}}} {\frac {5}{10}}. The fractions 1 5 {\displaystyle {\frac {1}{5}}} {\frac {1}{5}} and 1 10 {\displaystyle {\frac {1}{10}}} {\frac {1}{10}} are in their reduced, or simplified, form, because each is a unit fraction, with 1 as the numerator. You should know that 5 10 {\displaystyle {\frac {5}{10}}} {\frac {5}{10}} is not simplified, because 10 is a multiple of 5.

Consider the following problem. Franny says that 12 109 {\displaystyle {\frac {12}{109}}} {\frac {12}{109}} is a simplified fraction. Without making any calculations, how do you know she is correct? Since 109 is a prime number, you can tell that the fraction is simplified. 109 is only divisible by 109 and 1, so it shares no common factors with 12.

Determine which fraction is NOT simplified. Do not make any calculations: 4 5 {\displaystyle {\frac {4}{5}}} {\frac {4}{5}}, 4 7 {\displaystyle {\frac {4}{7}}} {\frac {4}{7}}, 4 8 {\displaystyle {\frac {4}{8}}} {\frac {4}{8}} Since 5 − 4 = 1 {\displaystyle 5-4=1} 5-4=1, you know that 4 5 {\displaystyle {\frac {4}{5}}} {\frac {4}{5}} is simplified. Since 7 is a prime number, you know that 4 7 {\displaystyle {\frac {4}{7}}} {\frac {4}{7}} is simplified. Since 8 is a multiple of 4, you know that 4 8 {\displaystyle {\frac {4}{8}}} {\frac {4}{8}} is NOT simplified.



















Comments
0 comment