
views
Perimeter Review

Perimeter is defined as the length surrounding a given area. Imagine you had a fence that runs around your entire property. In order to find the total length of the fence, you’d need to calculate the perimeter. Measuring the entire fence by hand is one way to do it, but an easier way is to use the perimeter formula. You might not be given the length of all 4 sides, which is another reason why you’d need to use an equation to find the perimeter instead of just addition.
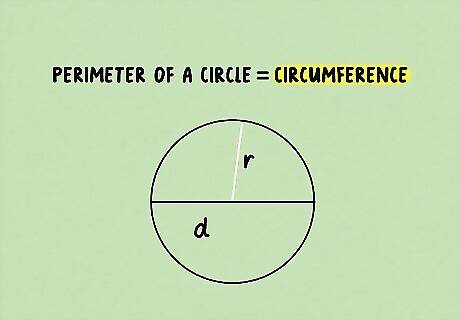
Circumference is the perimeter of a circle. Since a circle doesn’t have any straight lines, the method for figuring out its perimeter is a little bit different. It involves using Pi and the radius or diameter of the entire shape. You can’t find the perimeter of a circle just by measuring it; you have to use the circumference equation.

Express the perimeter in distance units. These are feet, inches, centimeters, miles, etc. Since you’re measuring the length of something, you always have to use real-world distance units when you get your answer. You’ll have to make sure all your units are the same before you do your equation, too. This might mean changing feet to inches, miles to feet, or anything in between.

Use an online calculator to check your answer. Although you might have to show your work on your homework or assignment, you can always use an online calculator to double check that you’re doing it right. Search for the shape you’re working on + perimeter in a web browser to find free online calculators that you can use. Make sure you’re using a calculator for your specific shape.
Finding the Perimeter of Rectangles (Including Squares)
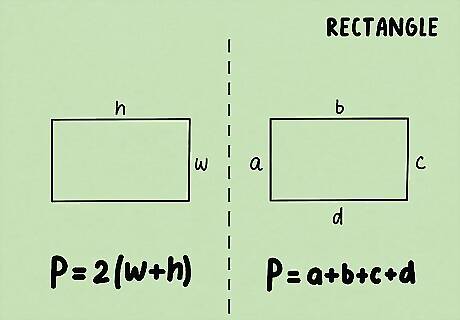
Set up the formula for the perimeter of a rectangle. The formula is P = 2 ( w + h ) {\displaystyle P=2(w+h)} P=2(w+h), where P {\displaystyle P} P equals the perimeter of the rectangle, w {\displaystyle w} w equals the width of the rectangle, and h {\displaystyle h} h equals the height of the triangle. If you don’t know the length of the width and height of the rectangle, you cannot use this formula. You can also use the formula P = a + b + c + d {\displaystyle P=a+b+c+d} P=a+b+c+d, where each variable is equal to the length of one side of the rectangle. A variable is any number in your equation that you use, signified by letters (a, b, c, d). If you don’t know the height and width of your shape, you can plug in the information you do know, like the area, the length of one side, or the length of the diagonal.
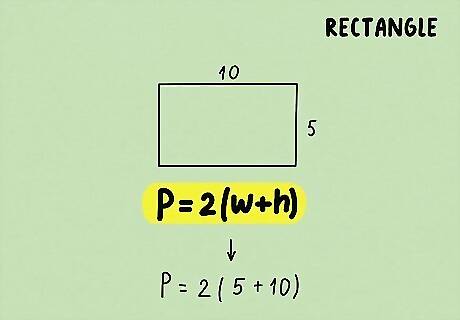
Plug the width and height into the formula. It doesn’t matter which measurement you use for the width and which you use for the height since the width and height are two adjacent sides. If the rectangle is not a square, these side lengths must be different. For example, if a rectangle has a width of 5 cm and a height of 10 cm, your formula will look like this: P = 2 ( 5 + 10 ) {\displaystyle P=2(5+10)} P=2(5+10).
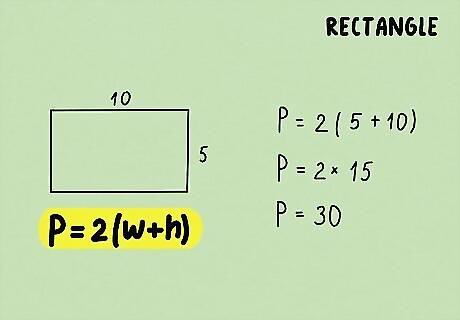
Add the length and width, and multiply by 2. Make sure you follow the order of operations and complete the calculation in parentheses before multiplying. The resulting value will give you the perimeter of your rectangle. For example: P = 2 ( 5 + 10 ) {\displaystyle P=2(5+10)} P=2(5+10) P = 2 ( 15 ) {\displaystyle P=2(15)} P=2(15) P = 30 {\displaystyle P=30} P=30So, the perimeter of the rectangle is 30 cm.
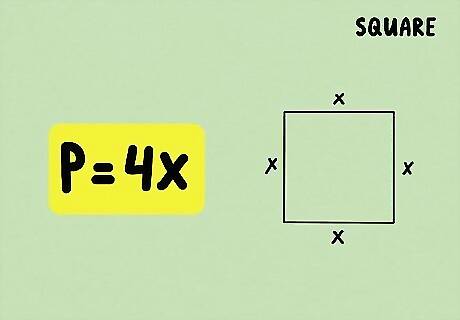
Use the formula P = 4 x {\displaystyle P=4x} P=4x to find the perimeter of a square. In this formula x {\displaystyle x} x is equal to the length of one side of the square. A square has 4 equal sides, so to find its perimeter, you only need to multiply the length of one side by 4. For example, if a square has one side that is 3 cm long, to find the perimeter, you would calculate P = 4 ( 3 ) = 12 {\displaystyle P=4(3)=12} P=4(3)=12. So, the perimeter is 12 cm.
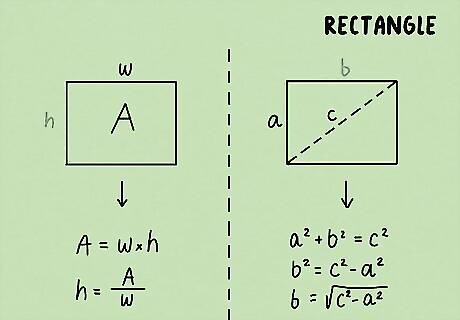
Find the perimeter given other information. Often you will not be given the length of all sides, or even the length of any side. It still may be possible to find the perimeter of a rectangle. If you know the area of the rectangle, and the length of one side, you can find the perimeter by finding the missing width or height using the area formula. Set up the formula A = w h {\displaystyle A=wh} A=wh. Plug in the values you know, then solve for the missing variable. Now you know the length and width, so you can use the perimeter formula. If you know one side length and the length of the diagonal, you can use the Pythagorean Theorem to find the missing side length. Set up the formula a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}} a^{{2}}+b^{{2}}=c^{{2}}. Substitute the length of the diagonal for c {\displaystyle c} c, and the side length for a {\displaystyle a} a. Solve for b {\displaystyle b} b. Now you know the length and width, so you can use the perimeter formula.
Finding the Perimeter of a Circle
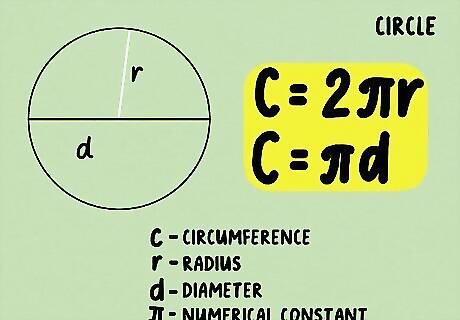
Set up the formula for finding the circumference of a circle. The circumference is the distance around the circle, and is thus the same as its perimeter. The formula is C = 2 π ⋅ r {\displaystyle C=2\pi \cdot r} C=2\pi \cdot r, where C {\displaystyle C} C equals the circumference and r {\displaystyle r} r equals the radius. Since the radius is half the diameter, you can use the formula C = π ( d ) {\displaystyle C=\pi (d)} C=\pi (d) if you have the diameter instead of the radius. When finding the perimeter of a circle, you don’t use the term perimeter, you use circumference. This is because circles don’t have any straight lines. Pi: A numerical constant, used in this formula to signify the constant numerical shape of a circle. Diameter: The length of the line through the center of the circle that touches both edges. Radius: The length of any line segment from the center of a circle out to the edge of the circle.
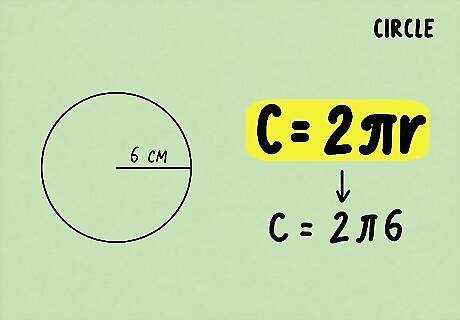
Plug the length of the radius into the formula. Write this in place of the variable r {\displaystyle r} r. If you are using the diameter formula, substitute for d {\displaystyle d} d. The length of the radius or diameter should be given, or you should be able to measure it. For example, if the radius of the circle is 6 cm, your formula will look like this: C = 2 π ⋅ 6 {\displaystyle C=2\pi \cdot 6} C=2\pi \cdot 6.

Multiply the radius by 2 π {\displaystyle 2\pi } 2\pi . You can use 3.14 for π {\displaystyle \pi } \pi , but if you are using a calculator you can use the π {\displaystyle \pi } \pi key for a more precise answer. The product of these three values is equal to the circumference, or perimeter, of the circle. For example: C = 2 π ⋅ 6 = 37.7 {\displaystyle C=2\pi \cdot 6=37.7} C=2\pi \cdot 6=37.7. So the circumference of the circle is 37.7 cm.
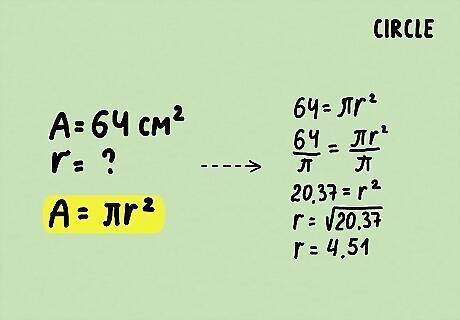
Find the perimeter given the area. The area of a circle is given by the formula A = π ⋅ r 2 {\displaystyle A=\pi \cdot r^{2}} A=\pi \cdot r^{{2}}. So, if you plug the area into the formula, you can solve for r {\displaystyle r} r. Once you have r {\displaystyle r} r, you can use the circumference formula to find the circumference. For example, if you are told that the area of a circle is 64 square centimeters, you would set up the formula 64 = π ⋅ r 2 {\displaystyle 64=\pi \cdot r^{2}} 64=\pi \cdot r^{{2}}. Then, solve for r {\displaystyle r} r: 64 = π ⋅ r 2 {\displaystyle 64=\pi \cdot r^{2}} 64=\pi \cdot r^{{2}} 64 π = π ⋅ r 2 π {\displaystyle {\frac {64}{\pi }}={\frac {\pi \cdot r^{2}}{\pi }}} {\frac {64}{\pi }}={\frac {\pi \cdot r^{{2}}}{\pi }} 20.37 = r 2 {\displaystyle 20.37=r^{2}} 20.37=r^{{2}} 20.37 = r 2 {\displaystyle {\sqrt {20.37}}={\sqrt {r^{2}}}} {\sqrt {20.37}}={\sqrt {r^{{2}}}} 4.51 = r {\displaystyle 4.51=r} 4.51=rSo, the radius of the circle is about 4.51 cm. Now you can plug this value into the perimeter formula and solve.
Finding the Perimeter of Triangles
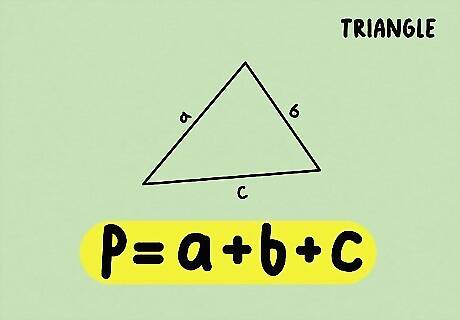
Set up the formula for finding the perimeter of a triangle. The formula is P = a + b + c {\displaystyle P=a+b+c} P=a+b+c, where the variables equal the three sides of the triangle. This formula is the same whether or not the triangle is right. You must have all side lengths to use this formula. If you know that you have an equilateral triangle, you only need one side length, since an equilateral triangle has three equal sides. For example, if a triangle has sides that are 5, 7, and 12 cm in length, you simply add up all the side lengths to find the perimeter: P = 5 + 7 + 12 = 24 {\displaystyle P=5+7+12=24} P=5+7+12=24. So, the perimeter of the triangle is 24 cm.

Find the perimeter of a right triangle with a missing side length. Sometimes you might be presented with a right triangle that only has two side lengths given. In this case, set up the Pythagorean formula to find the missing side length. The formula is a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}} a^{{2}}+b^{{2}}=c^{{2}}, where c {\displaystyle c} c is the length of the hypotenuse (the side opposite the right angle), and a {\displaystyle a} a and b {\displaystyle b} b are the other two side lengths. Solve for the missing variable, and this will give you your missing side length. For example, if you have a right triangle with a hypotenuse of 10 cm, and one side length of 6 cm, set up the Pythagorean formula like this: 6 2 + b 2 = 10 2 {\displaystyle 6^{2}+b^{2}=10^{2}} 6^{{2}}+b^{{2}}=10^{{2}} Solve for b {\displaystyle b} b: 36 + b 2 = 100 {\displaystyle 36+b^{2}=100} 36+b^{{2}}=100 36 + b 2 − 36 = 100 − 36 {\displaystyle 36+b^{2}-36=100-36} 36+b^{{2}}-36=100-36 b 2 = 64 {\displaystyle b^{2}=64} b^{{2}}=64 b 2 = 64 {\displaystyle {\sqrt {b^{2}}}={\sqrt {64}}} {\sqrt {b^{{2}}}}={\sqrt {64}} b = 8 {\displaystyle b=8} b=8 Now that you have all three side lengths, you can add them up to find the perimeter: 10 + 6 + 8 = 24 {\displaystyle 10+6+8=24} 10+6+8=24. So, the perimeter of the triangle is 24 cm.
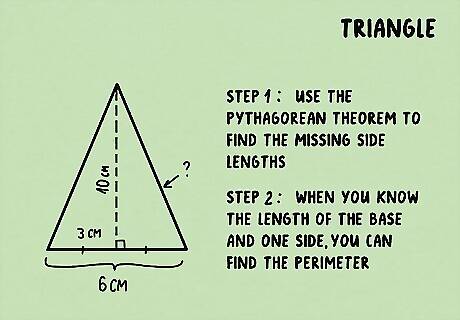
Find the perimeter of an isosceles triangle with a missing side length. An isosceles triangle is when the height, or the altitude, bisects the base. If you know the height and base of the triangle, you can use the Pythagorean theorem to find the missing side lengths. For example, if an isosceles triangle has a height of 10 cm and a base of 6 cm, you can think of the height creating two right triangles. Since the height bisects the base, one side length of the right triangle will be 3 cm. The other side length will be equal to the height: 10 cm. The missing side length is the hypotenuse. Set up the Pythagorean formula, plugging in the side lengths: 10 2 + 3 2 = c 2 {\displaystyle 10^{2}+3^{2}=c^{2}} 10^{{2}}+3^{{2}}=c^{{2}}. Make the necessary calculations to find the missing side length: 100 + 9 = c 2 {\displaystyle 100+9=c^{2}} 100+9=c^{{2}} 109 = c 2 {\displaystyle 109=c^{2}} 109=c^{{2}} 109 = c 2 {\displaystyle {\sqrt {109}}={\sqrt {c^{2}}}} {\sqrt {109}}={\sqrt {c^{{2}}}} 10.44 = c {\displaystyle 10.44=c} 10.44=c. An isosceles triangle has 2 equal sides. So, the perimeter of the triangle is equal to 2 x + b {\displaystyle 2x+b} 2x+b, where x {\displaystyle x} x equals the length of one side, and b {\displaystyle b} b equals the base. So, if you know the length of the base and one side, you can find the perimeter of an isosceles triangle: P = 2 ( 10.44 ) + 6 = 26.88 {\displaystyle P=2(10.44)+6=26.88} P=2(10.44)+6=26.88. So, the perimeter of the triangle is 26.88 cm.
Finding the Perimeter of a Regular Polygon
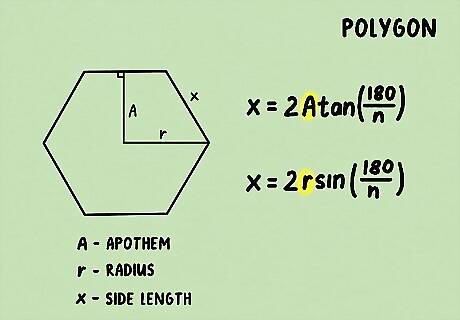
Find the length of one side. A regular polygon is a polygon that is equiangular and equilateral. You can find the length of one side if you know the length of the polygon’s apothem or radius. The apothem is the distance between the center of the polygon to the midpoint of any side, and the radius is the distance between the center of the polygon and any vertex. To find a side length given the apothem, use the formula x = 2 A tan ( 180 n ) {\displaystyle x=2A{\text{tan}}({\frac {180}{n}})} x=2A{\text{tan}}({\frac {180}{n}}), where x {\displaystyle x} x equals the side length and A {\displaystyle A} A equals the apothem. To find the side length given the radius, use the formula x = 2 r sin ( 180 n ) {\displaystyle x=2r{\text{sin}}({\frac {180}{n}})} x=2r{\text{sin}}({\frac {180}{n}}), where x {\displaystyle x} x equals the side length and r {\displaystyle r} r equals the radius. For example, if the radius of a hexagon is 5 cm, to find the side length, you would calculate: x = 2 ( 5 ) sin ( 180 6 ) {\displaystyle x=2(5){\text{sin}}({\frac {180}{6}})} x=2(5){\text{sin}}({\frac {180}{6}}) x = 2 ( 5 ) sin ( 30 ) {\displaystyle x=2(5){\text{sin}}(30)} x=2(5){\text{sin}}(30) x = 2 ( 5 ) ( .5 ) {\displaystyle x=2(5)(.5)} x=2(5)(.5) x = 5 {\displaystyle x=5} x=5
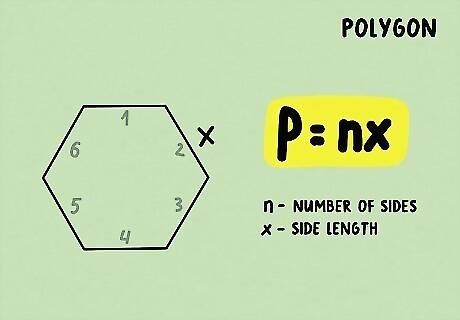
Set up the formula for the perimeter of a regular polygon. The formula is P = n x {\displaystyle P=nx} P=nx, where n {\displaystyle n} n is the number of sides the polygon has, and x {\displaystyle x} x is the length of one side.
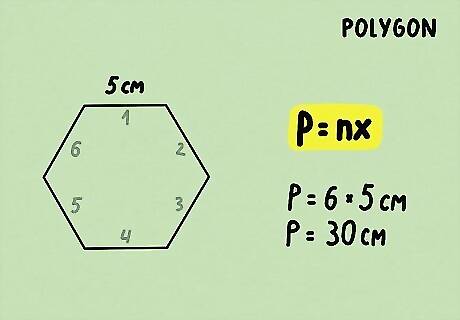
Plug the values of x {\displaystyle x} x and n {\displaystyle n} n into the formula. Multiply these two values to find the perimeter of the polygon. For example, if a regular hexagon has a side length of 5 cm, you would calculate P = ( 6 ) ( 5 ) = 30 {\displaystyle P=(6)(5)=30} P=(6)(5)=30. So, the perimeter of the hexagon is 30 cm.
Finding the Perimeter of an Ellipse
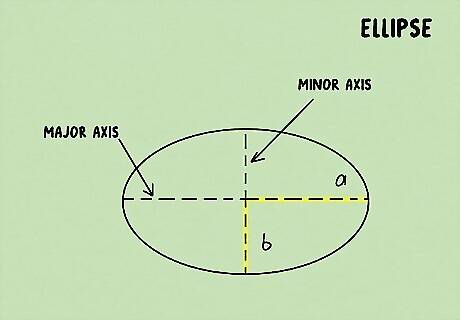
Measure the “sides” of your ellipse. An ellipse is an oval-shaped circle, so it doesn’t have any straight lines. To find the perimeter, you need to know the circumference of both the height and the width, or variables a and b. If you don’t know this information already, you can measure your ellipse on your own. Normally, variable a goes from left to right on the major axis, and variable b goes up and down on the minor axis.
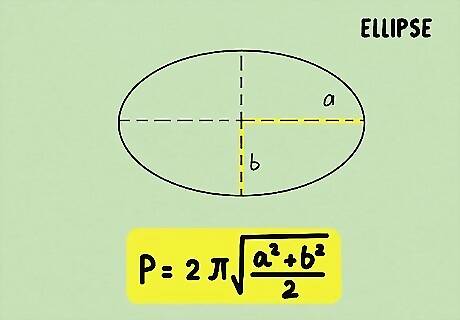
Plug the information into an equation. There are actually a few different equations that you can use to find the perimeter of an ellipse, and they all may give you a slightly different answer. The easiest formula to use is: p = 2 π ( a 2 + b 2 ) / 2 . {\displaystyle p=2\pi {\sqrt {(a^{2}+b^{2})/2}}.} {\displaystyle p=2\pi {\sqrt {(a^{2}+b^{2})/2}}.} This will give you an answer within 5% of the true perimeter of the ellipse. For example, if variable a is 3 and variable b is 2, your equation would look like this: p = 2 π ( 3 2 + 2 2 ) / 2 . {\displaystyle p=2\pi {\sqrt {(3^{2}+2^{2})/2}}.} {\displaystyle p=2\pi {\sqrt {(3^{2}+2^{2})/2}}.}
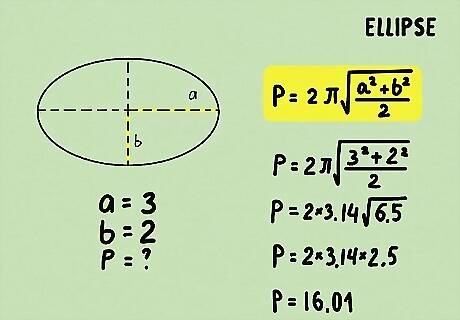
Solve the equation. Now you can use your inputted variables to find the perimeter of the ellipse. Remember that this is an approximate answer, not an exact one. For example, if the equation is p = 2 π ( 3 2 + 2 2 ) / 2 . {\displaystyle p=2\pi {\sqrt {(3^{2}+2^{2})/2}}.} {\displaystyle p=2\pi {\sqrt {(3^{2}+2^{2})/2}}.}, p = 2 π 18 {\displaystyle p=2\pi {\sqrt {18}}} {\displaystyle p=2\pi {\sqrt {18}}}, p = 16.01 {\displaystyle p=16.01} {\displaystyle p=16.01} rounded to 2 sig figs.
Finding the Perimeter of a Sector
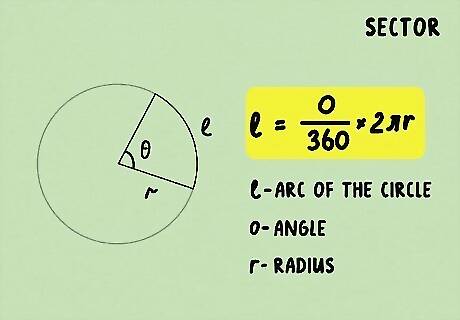
Find the length of the arc. A sector is a triangular slice taken from a whole circle (it looks like a piece of pizza). To start the equation, you need to find the length, or variable l, of the arc itself. If you aren’t given that information, you can solve for l with this equation: l = ( θ / 360 ) × 2 π r {\displaystyle l=(\theta /360)\times 2\pi r} {\displaystyle l=(\theta /360)\times 2\pi r}.
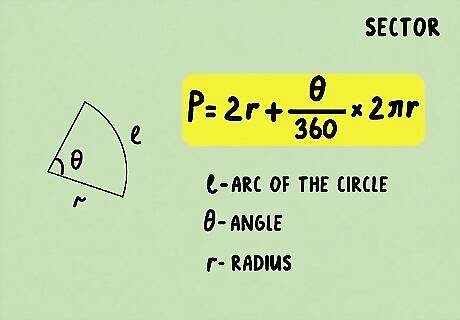
Plug the variables into the equation. To find the perimeter of a sector, plug your numbers into this equation: 2 r + ( θ / 360 ) × 2 π r {\displaystyle 2r+(\theta /360)\times 2\pi r} {\displaystyle 2r+(\theta /360)\times 2\pi r}, where “2r” is 2 times the radius and “θ” is the angle of the sector. Once you’ve done that, you can solve for the perimeter. For example, 2 × 4 + ( 60 / 360 ) × 2 × 3.14 × 4 {\displaystyle 2\times 4+(60/360)\times 2\times 3.14\times 4} {\displaystyle 2\times 4+(60/360)\times 2\times 3.14\times 4}.

Solve the equation. Once you’ve plugged in your variables, you can use the order of operations to solve for the perimeter. This is an exact number, so use the equal sign for your answer. 2 × 4 + ( 60 / 360 ) × 2 × 3.14 × 4 = 12.2 m m {\displaystyle 2\times 4+(60/360)\times 2\times 3.14\times 4=12.2mm} {\displaystyle 2\times 4+(60/360)\times 2\times 3.14\times 4=12.2mm}.
Finding the Perimeter of a Pentagon
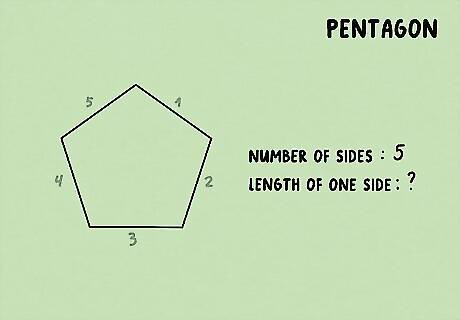
Find the number of sides and the length of one side. A pentagon always has 5 sides, so you’ll always be able to plug 5 into your equation. Then, all you need to find out is the length of one side to plug in for the variable.
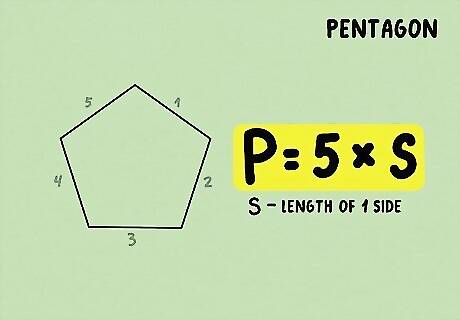
Plug the variables into the equation. The formula to find the perimeter of a pentagon is P = 5 × s {\displaystyle P=5\times s} {\displaystyle P=5\times s}. The variable “s” stands for the length of 1 side. For example, your equation might look like this: P = 5 × 10 {\displaystyle P=5\times 10} {\displaystyle P=5\times 10}.
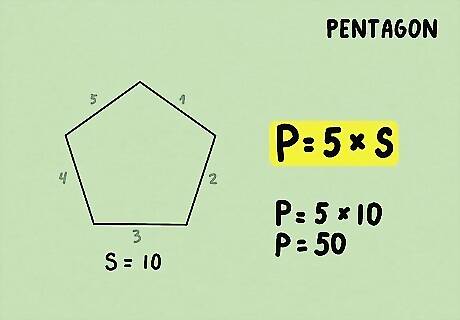
Solve for the perimeter. Once you’ve got your equation, you can use the formula to figure out the answer. Check your answer on a calculator to make sure it’s right. For example, P = 5 × 10 = 50 {\displaystyle P=5\times 10=50} {\displaystyle P=5\times 10=50}.
Finding the Perimeter of a Quadrilateral
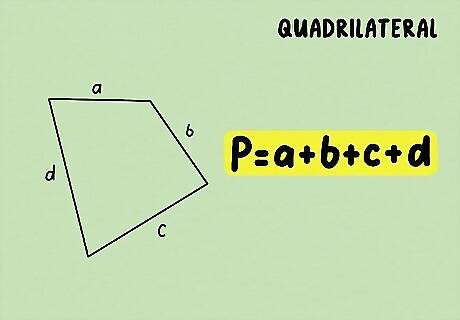
Find the length of all 4 sides. A quadrilateral looks like a rectangle with uneven sides. If you know all 4 sides of the quadrilateral, you can find the perimeter by adding them all up. If you don’t know the length of all 4 sides, you can use the information you do have to solve for variable x.
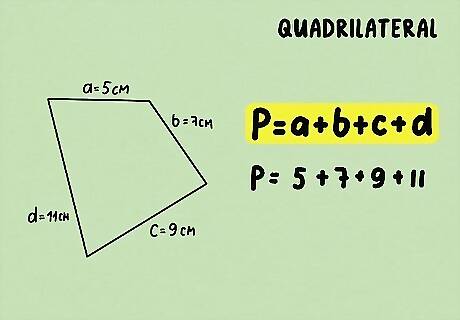
Plug the side lengths into your equation. To find the perimeter of a quadrilateral, you just need to add up the side lengths. The formula is P = ( a + b + c + d ) {\displaystyle P=(a+b+c+d)} {\displaystyle P=(a+b+c+d)}. For example, P = 5 + 7 + 9 + 11 {\displaystyle P=5+7+9+11} {\displaystyle P=5+7+9+11}.
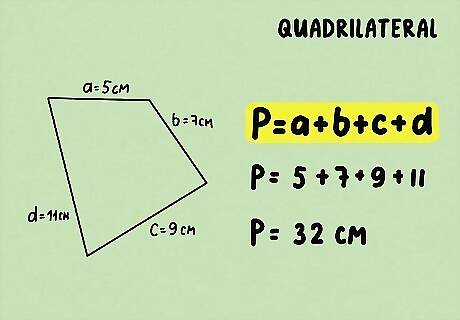
Add up the lengths to find the perimeter. Once you know all 4 side lengths, just add them up. Don’t forget to put your units on the end of your answer. For example, P = 5 + 7 + 9 + 11 = 32 c m {\displaystyle P=5+7+9+11=32cm} {\displaystyle P=5+7+9+11=32cm}.


















Comments
0 comment