views
Understanding the Rules

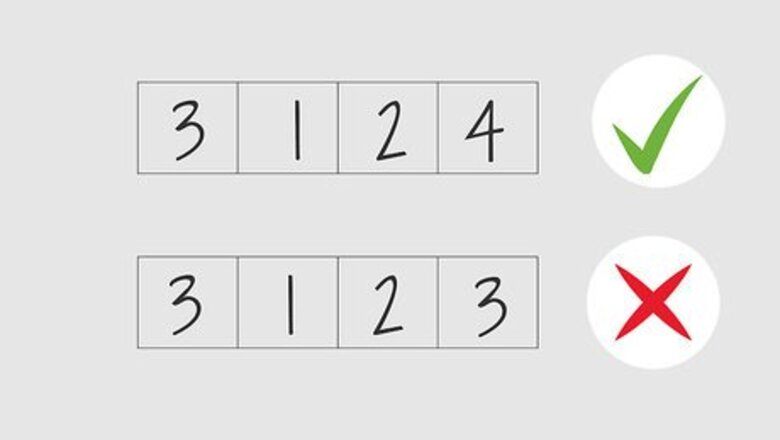
Fill in each horizontal row with the numbers 1-4, without repeating any of them. This is where Kenken gets its similarity to Sudoku. If you have a four square by four square grid, every single horizontal row must have a 1, 2, 3, and a 4 in it. The numbers, of course, can be in any order. This is true for each row. If your grid is a six by six, you would have the numbers 1, 2, 3, 4, 5, and 6, without any repeating. If it is a 9x9, then 1-9, etc.
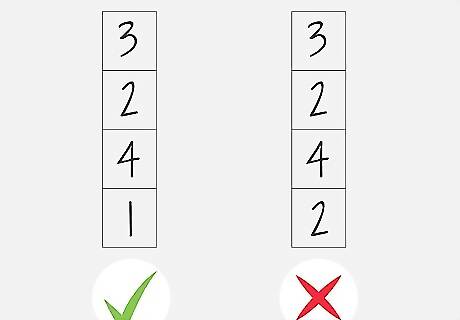
Fill each vertical column with every number, without repeating. A completed Kenken needs to have every single number in every single row and column, only once. Note, however, that this doesn't just mean you fill in every single box with your numbers and win -- each puzzle still requires a specific order -- as dictated by "cages."
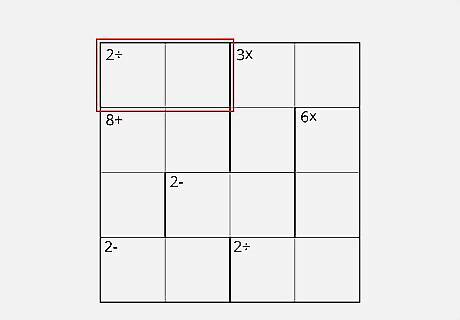
Find and note the "cages," thick, irregular boxes within the Kenken, to get clues to a solution. Inside of the Kenken, there are big, thick lines marking of several boxes at once, with a mathematical equation (ex. "3+," "1-," "2"). These are called cages, and they provide the puzzle and the solution. Make a note of them, making sure you understand what boxes they cover. Cages can be straight, composed of either a single block or many at once, or L-shaped. Just follow the big, thick lines. Before beginning, make sure you can tell the edges of the each cage to prevent mistakes. Every box will be in a cage of some sort.
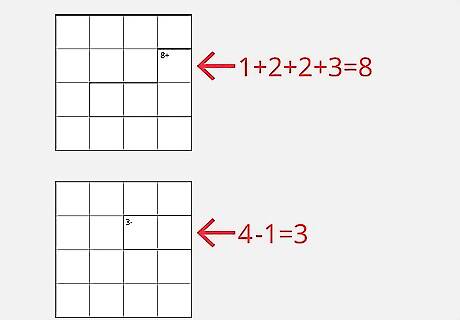
Know that the number and syllable at the top of each cage must be the "goal," or answer, of the written numbers put inside. If you have four numbers in a cage labeled "8+," then the four numbers in that cage must add up to eight, like 1 | 2 | 2 | 3 (note that this would be an L-shaped cage, otherwise you'd have two 2s in the same line!). So a cage with two boxes labeled "3-" would have to have two numbers that, when subtracted, equal 3, like 4 and 1. Every cage will have a goal -- and this is how you solve Ken Ken. Kenken only contains addition (+), subtraction (-), multiplication (×), and division (÷). Cages with only one box and no mathematical symbol ("4") mean you just place the number in the box on its own. If the box just says "4," just put a 4 in the box.
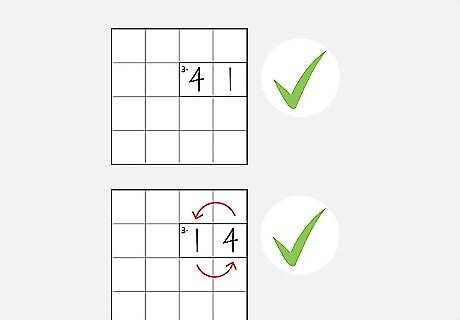
Know that subtraction and division boxes can be in any order. If you have a box that asks for "2÷," you can answer it with either "4 | 2" or "2 | 4." You just need the two correct numbers in the equation -- the order doesn't matter.
Know that the same rules apply no matter how big the puzzle gets. These rules all still apply no matter if you're playing a 4x4 or a 9x9. While the difficulty of the puzzle increases depending on the size, the actual rules and strategy for solving it do not. If you're a beginner, start with 4x4 boards to get used to the system and strategy. Some papers even offer 3x3 grids for beginners too.
Solving Kenken Successfully
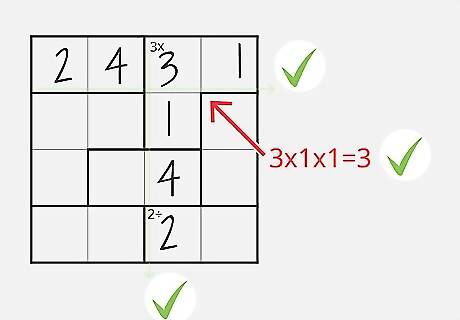
Always check all three sets of clues before putting in a number. Remember, you have to pay attention to three separate rules when inputting numbers, but this is to your advantage. Very few numbers satisfy all three conditions, and this is where your solution comes from: Only one of each number in each horizontal row. Only one of each number in each vertical column. The answer of each cage matches the number and mathematical symbol in the upper left corner.
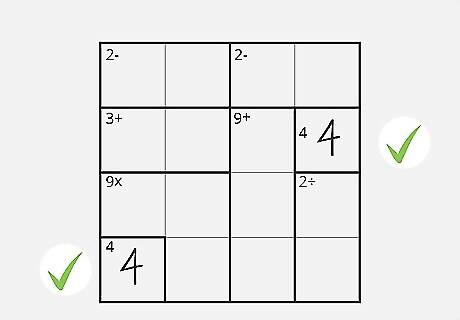
Fill in blank single boxes first. Take all of the basic boxes without mathematical symbols first, like "2," or "9" and simply fill in the number. If the box just says two, put in a two. This will take care of the basics and start to reveal other answers.
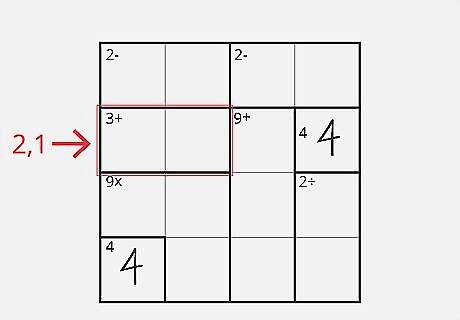
Find and mark the boxes that only have one potential answer. This will depend on the size of the board, but you'll still find them easily with some practice. For example, imagine a 4x4 puzzle. Take a two box cage for "3-." Knowing that you only have 1, 2, 3, and 4 to choose from, you know that there is only one pair that subtracts to three, 4 and 1. While you might not know the order, you do know these are the only two numbers in this row. Make a note of them for later. Every Kenken has some of these "easy" boxes to get you started, such as: Multiplication/division by grid size and odd numbers usually only has a few answers. Examples include "4x" in a 4x4 grid (1 & 4), "15x" in a 6x6 grid (3 & 5), etc. Two-box addition cages, usually for 3+ or 4+ (can only use 1, 2, and 3).
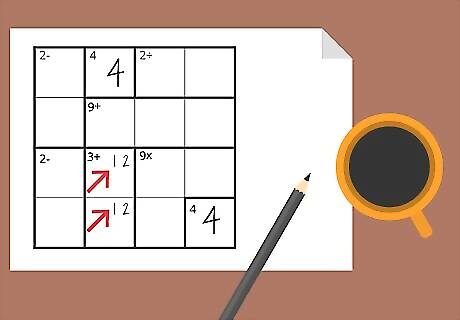
Write smaller numbers in the upper right corner to take notes, crossing them off as they are eliminated. There are a lot of places where two numbers will equally plausible, as you don't know enough about the rest of the board to figure out which number is correct. Write small notes in the upper right corner of the box, allowing you to see which numbers could be in each place, and which numbers have to be there. For example: In the previous step, you noted that you need a 4 and a 1 to make 3-, but you didn't know what order. But if the same row as the top box already contains a 4, then suddenly it's all clear. The 1 goes on top, and the 4 goes below, making your "3-."
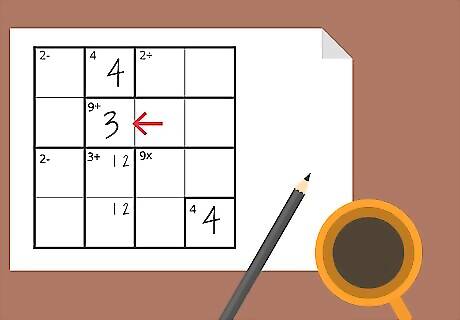
Use groupings of potential numbers to fill in the areas you're unsure of. For example, imagine a vertical row that already contains a 4 and a blank in the top boxes. The bottom two boxes are a cage for "3+," which can only be created with a 1 and a 2. This means the second box must be a 3, even though you don't know what order the 1 and 2 are. The finished cage would look like this: 4 3 1 or 2 1 or 2
Using Advanced Strategies
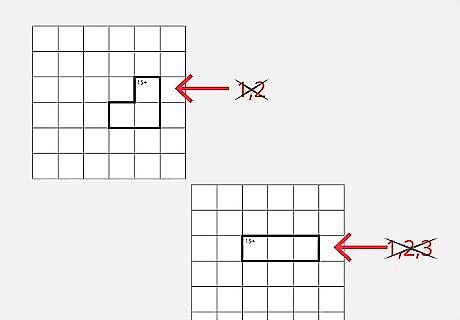
Keep track of which numbers you cannot use in bigger Kenken puzzles. If you've got a three box "15+" cage in a 6x6 grid, you can't use a 1 or 2. Ever. You simply couldn't add any other two numbers up with 1 or 2 to get top 15. If the cage isn't L-shaped, you can't even use a 3, since only 6+6+3 = 15 and you can't use two sixes in a row. This may seem like useless information, but it means that the row or column must have its 1, 2, or 3 further down. By knowing you can't use them in the cage, you also tell yourself that they must be used further down the line.
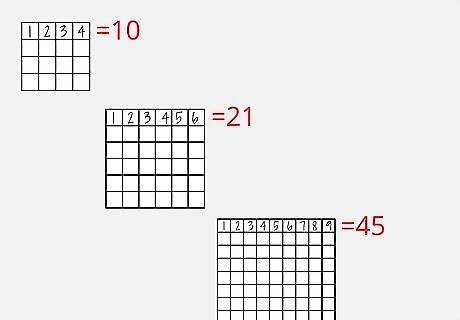
Understand the total sum of each row, and use the current numbers in it, to tackle tricky areas. Best shown in an example, imagine a row 6-box row. Since it must contain the numbers 1-6, each row will always add up to 21 (1 + 2 + 3 + 4 + 5 + 6 = 21). Now imagine a 4 box, 12+ cage in that row. You might not know which four numbers add up to 12, but you do know that the other two boxes must add up to 9, since the whole row must equal 21, and you know that part of it adds up to 12. This means your top box can suddenly contain only 2 pairs -- 3 & 6 or 4 & 5. 4 x 4 puzzle rows must add up to 10. 6 x 6 puzzle rows must add up to 21. 9 x 9 puzzle rows must add up to 45. Talented puzzlers can do the same thing with multiplication, too. For example, each row of a 6x6 must multiply to 720. If you have a big product in one row, find out what you have left to eliminate numbers.
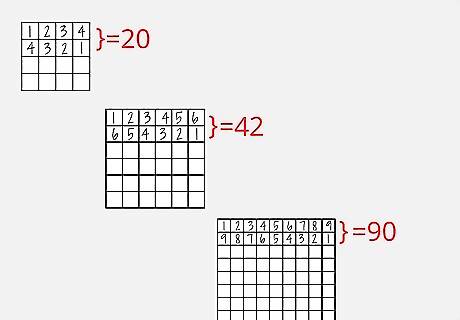
Expand the row by row sums above to account for 2-3 rows at once. The strategy above is great for single row problems, but any non-linear cages and you'll be lost. However, remember that each row of a 6x6 equals 21, meaning that any two rows must equal 42. Similarly, if the product of one row is 720, then the product of two rows must be 720. If you've got some cages with big sums or products ("20+," "45x"), you can subtract or divide these out to make the rest of the rows easier to solve.
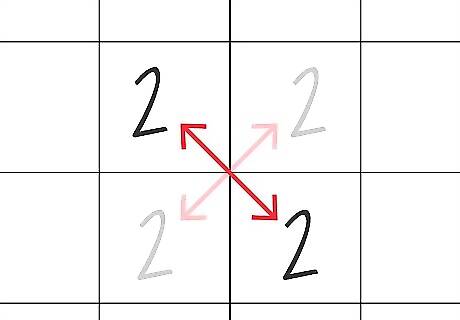
Notice "X-wing pairs" to eliminate potential locations for numbers. For difficult Kenkens, erasing possibilities is just as important as finding the right numbers. The "X-wing" is when you have the same possible number (say, a 2) in two side-by-side boxes in two different places (see example below). You might not know which one goes where, but know that two of those four boxes contain a 2. If a two is in the left box on one row, then it must be on the right box of the other row (because you can only have one 2 in each row). However, X-winging is when you can eliminate all 2s from every other space in the two rows (shown by the "X"). A two must be in the top or bottom -- meaning it cannot be in the middle rows. You can therefore eliminate any twos in between: 2 or 4 | 2 or 3 X | X X | X 2 or 3 | 2 or 1




















Comments
0 comment