
views
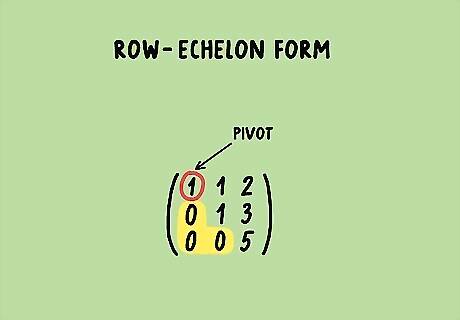
Understand what row-echelon form is. The row-echelon form is where the leading (first non-zero) entry of each row has only zeroes below it. These leading entries are called pivots, and an analysis of the relation between the pivots and their locations in a matrix can tell much about the matrix itself. An example of a matrix in row-echelon form is below. ( 1 1 2 0 1 3 0 0 5 ) {\displaystyle {\begin{pmatrix}1&1&2\\0&1&3\\0&0&5\end{pmatrix}}} {\begin{pmatrix}1&1&2\\0&1&3\\0&0&5\end{pmatrix}}
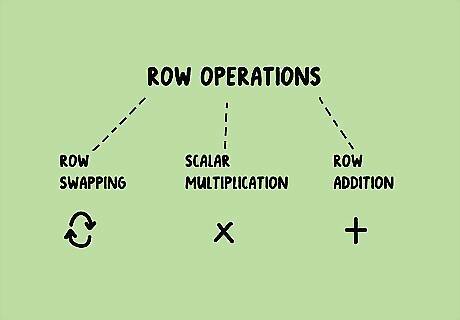
Understand how to perform elementary row operations. There are three row operations that one can do to a matrix. Row swapping. Scalar multiplication. Any row can be replaced by a non-zero scalar multiple of that row. Row addition. A row can be replaced by itself plus a multiple of another row.

Begin by writing out the matrix to be reduced to row-echelon form. ( 1 1 2 1 2 3 3 4 5 ) {\displaystyle {\begin{pmatrix}1&1&2\\1&2&3\\3&4&5\end{pmatrix}}} {\begin{pmatrix}1&1&2\\1&2&3\\3&4&5\end{pmatrix}}
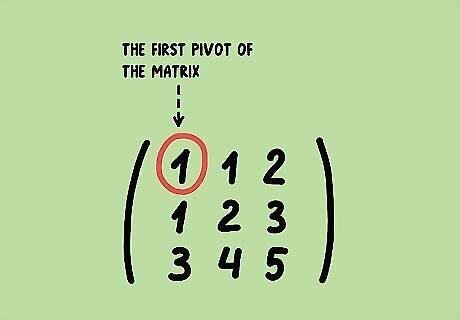
Identify the first pivot of the matrix. The pivots are essential to understanding the row reduction process. When reducing a matrix to row-echelon form, the entries below the pivots of the matrix are all 0. For our matrix, the first pivot is simply the top left entry. In general, this will be the case, unless the top left entry is 0. If this is the case, swap rows until the top left entry is non-zero. By their nature, there can only be one pivot per column and per row. When we selected the top left entry as our first pivot, none of the other entries in the pivot's column or row can become pivots.
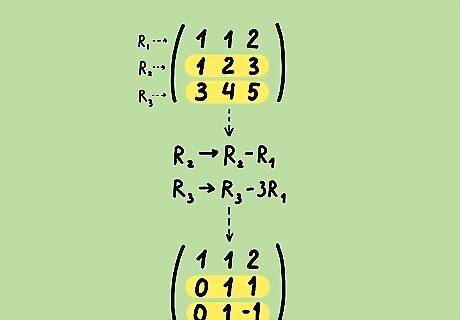
Perform row operations on the matrix to obtain 0's below the first pivot. For our matrix, we want to obtain 0's for the entries below the first pivot. Replace the second row with itself minus the first row. Replace the third row with itself minus three times the first row. These row reductions can be succinctly written as R 2 → R 2 − R 1 {\displaystyle R_{2}\to R_{2}-R_{1}} R_{{2}}\to R_{{2}}-R_{{1}} and R 3 → R 3 − 3 R 1 . {\displaystyle R_{3}\to R_{3}-3R_{1}.} R_{{3}}\to R_{{3}}-3R_{{1}}. ( 1 1 2 0 1 1 0 1 − 1 ) {\displaystyle {\begin{pmatrix}1&1&2\\0&1&1\\0&1&-1\end{pmatrix}}} {\begin{pmatrix}1&1&2\\0&1&1\\0&1&-1\end{pmatrix}}

Identify the second pivot of the matrix. The second pivot can either be the middle or the middle bottom entry, but it cannot be the middle top entry, because that row already contains a pivot. We will choose the middle entry as the second pivot, although the middle bottom works just as well.
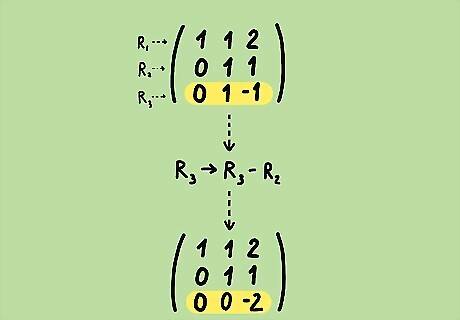
Perform row operations on the matrix to obtain 0's below the second pivot. R 3 → R 3 − R 2 {\displaystyle R_{3}\to R_{3}-R_{2}} R_{{3}}\to R_{{3}}-R_{{2}} ( 1 1 2 0 1 1 0 0 − 2 ) {\displaystyle {\begin{pmatrix}1&1&2\\0&1&1\\0&0&-2\end{pmatrix}}} {\begin{pmatrix}1&1&2\\0&1&1\\0&0&-2\end{pmatrix}} This matrix is in row-echelon form now.
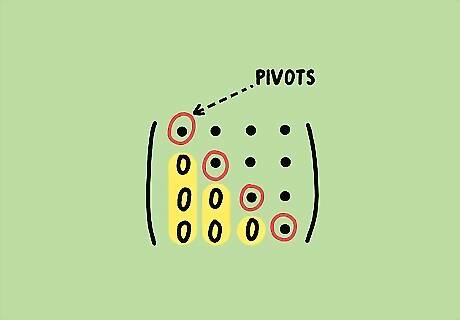
In general, keep identifying your pivots. Row-reduce so that the entries below the pivots are 0.




















Comments
0 comment