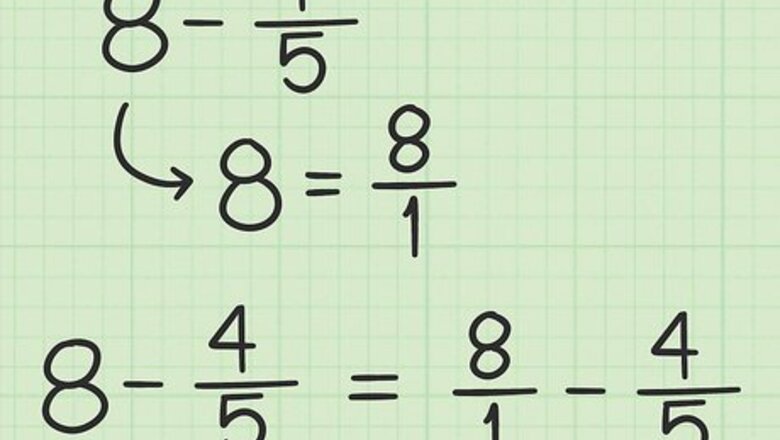
views
Subtracting Fractions from Whole Numbers
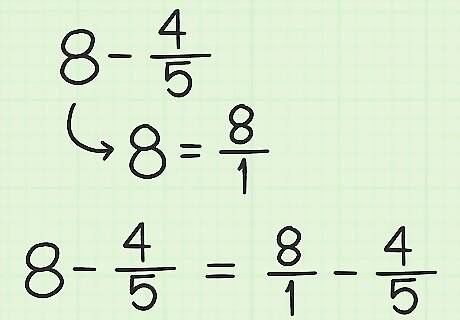
Convert the whole number to a fraction.To do this, give the whole number a denominator of 1. Example: 8 − 4 5 {\displaystyle 8-{\frac {4}{5}}} 8-{\frac {4}{5}} = 8 1 − 4 5 {\displaystyle ={\frac {8}{1}}-{\frac {4}{5}}} ={\frac {8}{1}}-{\frac {4}{5}}
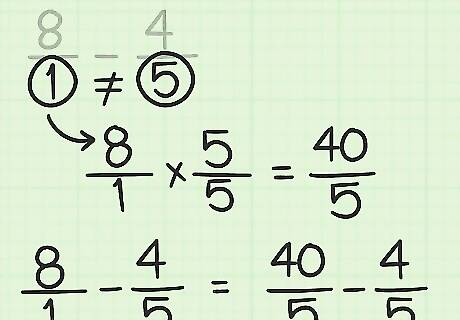
Convert to fractions of like denominators. The original fraction's denominator is also the least common denominator (LCD) of the two fractions. Multiply the top and bottom of the "whole number fraction" by this number so the fractions have the same denominator. 8 1 − 4 5 {\displaystyle {\frac {8}{1}}-{\frac {4}{5}}} {\frac {8}{1}}-{\frac {4}{5}} = 8 ∗ 5 1 ∗ 5 − 4 5 {\displaystyle ={\frac {8*5}{1*5}}-{\frac {4}{5}}} ={\frac {8*5}{1*5}}-{\frac {4}{5}} = 40 5 − 4 5 {\displaystyle ={\frac {40}{5}}-{\frac {4}{5}}} ={\frac {40}{5}}-{\frac {4}{5}}
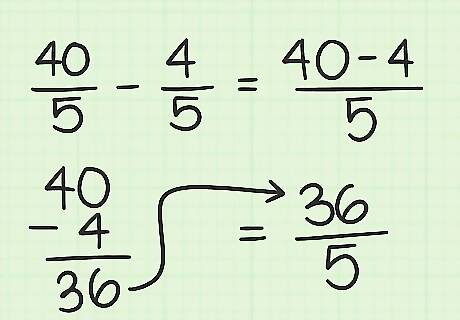
Subtract the numerators. Now that the fractions have the same denominators, you can treat the numerators as a normal subtraction problem: 40 5 − 4 5 {\displaystyle {\frac {40}{5}}-{\frac {4}{5}}} {\frac {40}{5}}-{\frac {4}{5}} = 40 − 4 5 {\displaystyle ={\frac {40-4}{5}}} ={\frac {40-4}{5}} = 36 5 {\displaystyle {\frac {36}{5}}} {\frac {36}{5}}
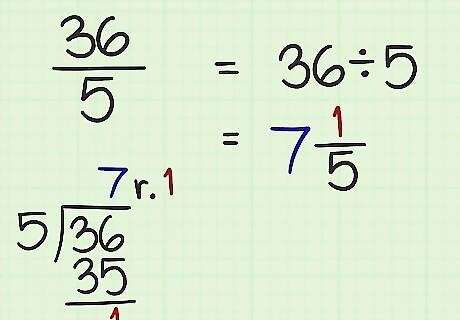
Convert to a mixed number (optional). If your answer is an improper fraction, you may need to rewrite it as a mixed number: Example: Rewrite 36 5 {\displaystyle {\frac {36}{5}}} {\frac {36}{5}} as a mixed number. How many times does 5 fit evenly into 36? 5 x 7 = 35, so the whole number portion is 7. What's left over? The whole number portion is equivalent to 35 5 {\displaystyle {\frac {35}{5}}} {\frac {35}{5}}, so solve 36 5 {\displaystyle {\frac {36}{5}}} {\frac {36}{5}} - 35 5 {\displaystyle {\frac {35}{5}}} {\frac {35}{5}} = 1 5 {\displaystyle {\frac {1}{5}}} {\frac {1}{5}} Combine the whole number and fraction: 36 5 {\displaystyle {\frac {36}{5}}} {\frac {36}{5}} = 7 1 5 {\displaystyle 7{\frac {1}{5}}} 7{\frac {1}{5}}
Alternate Method
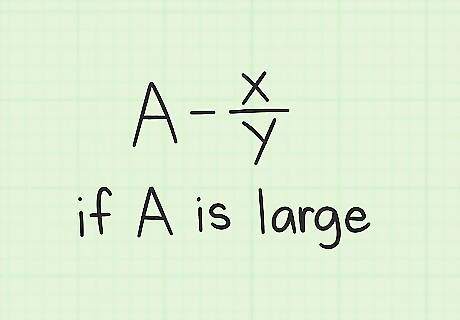
Try this for large whole numbers. Did you see how the method above converts the whole number into a fraction, then converts back to a mixed number at the end? This method lets you skip some of that so the fraction only involves smaller numbers.
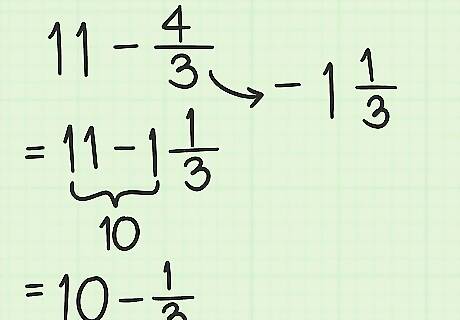
Convert improper fractions to mixed numbers. Skip this step if your fraction is not improper. (An improper fraction has a larger number on top than on bottom.) Example: 11 − 4 3 {\displaystyle 11-{\frac {4}{3}}} 11-{\frac {4}{3}} = 11 − 1 1 3 {\displaystyle =11-1{\frac {1}{3}}} =11-1{\frac {1}{3}} = 10 − 1 3 {\displaystyle =10-{\frac {1}{3}}} =10-{\frac {1}{3}}
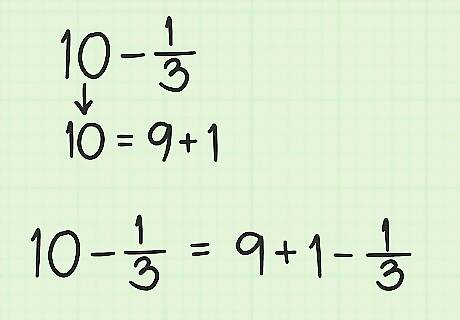
Separate the whole number into 1 and another whole number. For example, rewrite 5 as 4 + 1, or rewrite 22 as 21 + 1. 10 − 1 3 {\displaystyle 10-{\frac {1}{3}}} 10-{\frac {1}{3}} = 9 + 1 − 1 3 {\displaystyle =9+1-{\frac {1}{3}}} =9+1-{\frac {1}{3}}
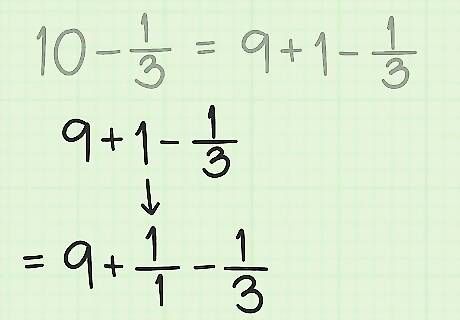
Convert the 1 into a fraction. At this point we're using the method above to solve the part of the problem in the form "1 - (fraction)". The other whole number will stay the same for the rest of the problem. = 9 + 1 − 1 3 {\displaystyle =9+1-{\frac {1}{3}}} =9+1-{\frac {1}{3}} = 9 + 1 1 − 1 3 {\displaystyle =9+{\frac {1}{1}}-{\frac {1}{3}}} =9+{\frac {1}{1}}-{\frac {1}{3}}
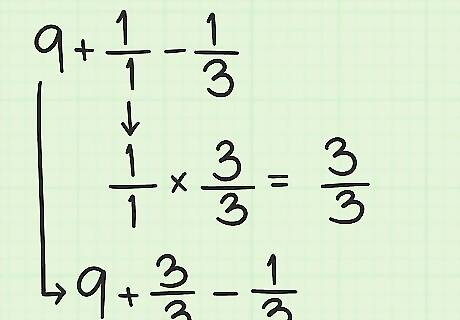
Multiply to give the fractions like denominators. As described above, multiply the top and bottom of your new fraction so it has the same denominator as the original fraction. = 9 + 1 ∗ 3 1 ∗ 3 − 1 3 {\displaystyle =9+{\frac {1*3}{1*3}}-{\frac {1}{3}}} =9+{\frac {1*3}{1*3}}-{\frac {1}{3}} = 9 + 3 3 − 1 3 {\displaystyle =9+{\frac {3}{3}}-{\frac {1}{3}}} =9+{\frac {3}{3}}-{\frac {1}{3}}
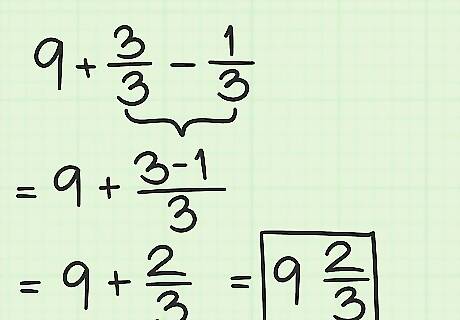
Combine the two fractions. Subtract the numerators to solve the fraction part of the equation. = 9 + 3 − 1 3 {\displaystyle =9+{\frac {3-1}{3}}} =9+{\frac {3-1}{3}} = 9 + 2 3 {\displaystyle =9+{\frac {2}{3}}} =9+{\frac {2}{3}} = 9 2 3 {\displaystyle =9{\frac {2}{3}}} =9{\frac {2}{3}}

















Comments
0 comment