Plotting the Mandelbrot Set by Hand: A Simple How-To Guide

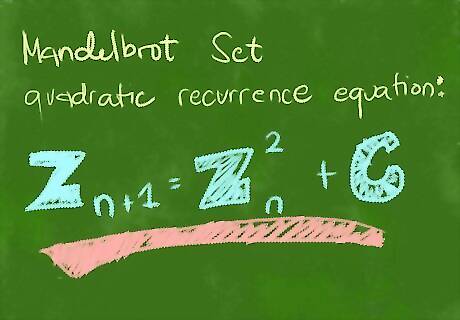
Understand the basic formula, often expressed as z = z + c. This simply means that, for each point in the Mandelbrot universe we wish to see, we keep calculating z until one of two conditions occur; then we color it to show how many calculations we made. Don't worry! This will become clear in the following steps.

Get 3 different-colored pencils, or crayons, or felt-tipped markers, plus a black pencil or pen to make the outline. The reason we want three colors is because we'll make a first approximation with no more than 3 iterations (passes, or in other words, applying the formula up to 3 times per point):

With the black marker, draw a large tic-tac-toe board, 3 by 3 squares, on a piece of paper.

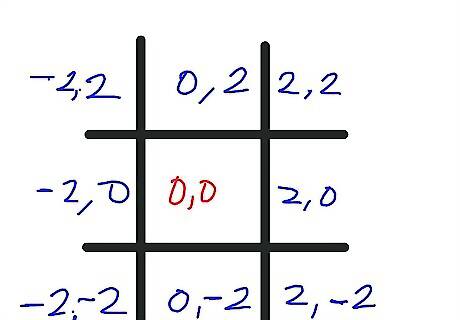
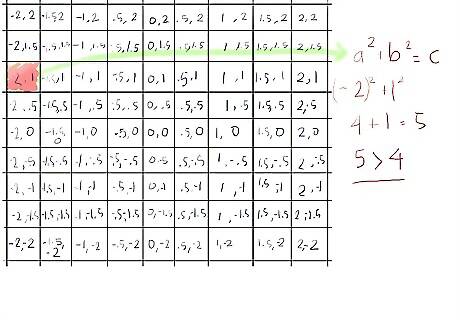
Label (also in black) the middle square (0, 0). This is the constant (c) value of the point in the exact center of the square. Now let's say each square is 2 units wide, so add and/or subtract 2 to/from the x and y values of each square, with x being the first number and y being the second number. When done, it will look like what you see displayed here. Whenever you follow the cells across, the y-values (the second number) should be the same; whenever you follow the cells down, the x-values (the first number) should be the same.

Calculate the first pass, or iteration, of the formula. You, as the computer (actually, the original meaning of the word was "a person who computes") can do this yourself. Let's start with these assumptions: The starting z value of each square is (0, 0). When the absolute value of z, for a given point, is greater than or equal to 2, that point (and its corresponding square) is said to have escaped the Mandelbrot set. When that happens, you will color the square according to the number of iterations of the formula you have applied to that point. 217503 5a.jpg Choose the colors you will use for pass 1, pass 2, and pass 3. Let's assume red, green, and blue, respectively, for purposes of this article. 217503 5b.jpg Calculate the value of z for the top-left corner of the tic-tac-toe board, assuming a starting z value of 0+0i or (0, 0) (see Tips for a better understanding of these representations). We are using the formula z = z + c as outlined in the first step. You will quickly see that, in this case, z+c is simply c, since zero squared is still zero. And what is c for this square? (-2, 2). 217503 5C.jpg Determine the absolute value of this point; the absolute value of a complex number (a, b) is the square root of a + b. Now, since we'll be comparing this to a known value: 2, we can avoid taking square roots by comparing a + b to 2, which we know equals 4. In this calculation, a = -2 and b = 2.217503 5D.jpg ([-2] + 2) = (4 + 4) = 8, which is greater than 4. It has escaped the Mandelbrot set after the first calculation, since its absolute value is greater than 2. Color it with the pencil you chose for pass 1. 217503 5e.jpg Mandelbrot_set_419.jpg Do the same for each square on the board, except for the center square, which will not escape the Mandelbrot set by the 3rd pass (nor will it ever escape). So you've only used two colors: the pass 1 color for all the outer squares, and the pass 3 color for the middle square.

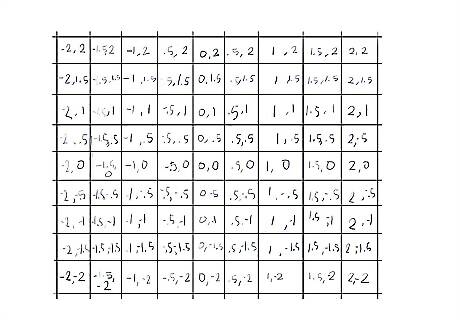
Let's try a square 3 times bigger, 9 by 9, but still keeping a maximum of 3 iterations.

Start with the 3rd row down, because that's where it gets interesting right away. The first element, (-2, 1) is greater than 2 (because (-2) + 1 turns out to be 5) so let's paint that one red, as it escapes the Mandelbrot set on the first pass. 217503 7a.jpg The second element, (-1.5, 1) turns out not to be greater than 2. Applying the formula for absolute value, x+y, with x = -1.5 and y = 1:217503 7b.jpg (-1.5) = 2.25 1 = 1 2.25 + 1 = 3.25, less than 4, so the square root is less than 2. So we move on to our second pass, calculating z+c using the shortcut (x-y, 2xy) for z (see Tips for how this shortcut is derived), still with x = -1.5 and y = 1: 217503 7c.jpg (-1.5) - 1 becomes 2.25 - 1, which becomes 1.25; 2xy, since x is -1.5 and y is 1, becomes 2(-1.5), which yields -3.0; This gives us a z of (1.25, -3) Now add c for this cell (add x to x, y to y) yielding (-0.25, -2) Let's test if its absolute value is now greater than 2:. Calculate x + y:217503 7d.jpg (-.25) = .0625 -2 = 4 .0625 + 4 = 4.0625, the square root of which is greater than 2, thus it has escaped after the second iteration: our first green! As you become familiar with the calculations, you'll sometimes be able to tell which ones escape the Mandelbrot set just by glancing at the numbers. In this example, the y component has a magnitude of 2, which when squared and added to the squared value of the other number, will be greater than 4. Any number greater than 4 will have a square root greater than 2. See the Tips below for a more detailed explanation. The third element, with a c value of (-1, 1) does not escape the first pass: since both 1 and -1 when squared is 1, x+y is 2. So we calculate z+c, using the shortcut (x-y, 2xy) for z:217503 7e.jpg (-1)-1 becomes 1-1, which is 0; 2xy is then 2(-1) = -2; z = (0, -2) adding c we get (0, -2) + (-1, 1) = (-1, -1) That's still the same absolute value as before (the square root of two, about 1.41); continuing with a third iteration:217503 7f.jpg ([-1])-([-1]) becomes 1-1, which is 0 (yet again)... but now 2xy is 2(-1)(-1), which is positive 2, yielding a z value of (0, 2) adding c we get (0, 2) + (-1, 1) = (-1, 3), which has an a + b of 10, much greater than 4. Thus this one also escapes. Color the cell in with your third color, blue, and move on to the next one, since we have completed three iterations with this point.217503 7g.jpg The fact that we're using only three colors becomes apparent as a problem here, since something that escapes after only 3 iterations is colored the same as (0, 0) which never escapes; obviously we still won't see anything close to the Mandelbrot "bug" at this level of detail.

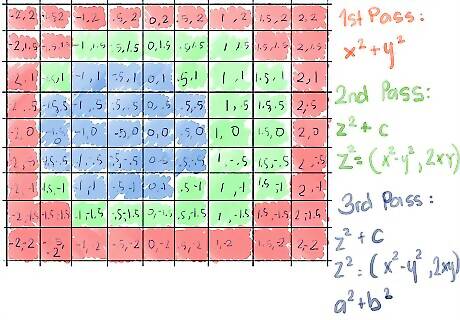
Continue calculating each cell until it has escaped, or you have reached the maximum number of iterations (the number of colors you're using: 3 in this example), at which point you color it. Here's how the 9 by 9 matrix looks after 3 iterations on each square...Looks like we're onto something!

Iterate the same matrix again with more colors (iterations) to reveal the next few layers, or better, draw up a much larger matrix for a longer-term project! You get more accurate pictures by: Mandelgen_81_81_0_0_1_rgb_fast_533.jpgIncreasing the number of cells; this has 81 cells per side. Note the similarity to the 9 by 9 matrix above, but the much smoother edges on the circle and oval. Mandelgen_81_81_0_0_1_rgb2black_fast_797.jpgIncreasing the number of colors (iterations); this has 256 shades each of red, green, and blue for a total of 768 colors compared to 3. Note that you can now see the outline of the well-known Mandelbrot "lake" (or "bug", depending on how you look at it). The downside is the amount of time it takes; if you can calculate each iteration in 10 seconds, that's about 2 hours for each cell in, or close to, the Mandelbrot lake. Though that's a relatively small part of the 81 by 81 matrix, it would still probably take a year to complete it, even if you worked on it for several hours each day. This is where the silicon type of computer comes in handy.